Logistic

使用方法：曲线拟合，分两个class，？基本只能处理数据点？

使用范围：都可以用。基本一根线能分就能分

input space

X=Rd\mathcal{X}=\mathbb{R}^d

label space / output space（y的范围是0到1）

Y=[0,1]\mathcal{Y}=[0,1]

hypothesis class F

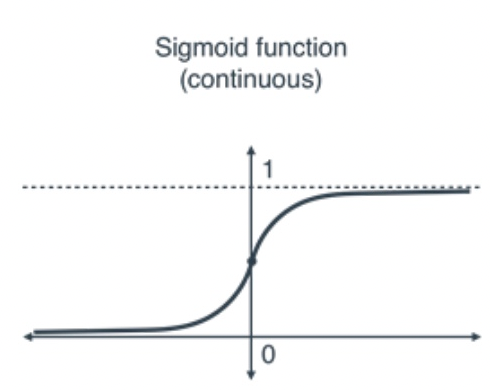
F:={x↦sigmoid(w⊤x+b) ∣ w∈Rd,b∈R},where sigmoid(a)=11+exp⁡(−a)\mathcal{F}:=\{x \mapsto sigmoid(w^\top x+b)\ |\ w\in\mathbb{R}^d,b\in\mathbb{R}\},\text{where }sigmoid(a)=\frac{1}{1+\exp(-a)}

注：ω\omega：weight vector；bb：bias

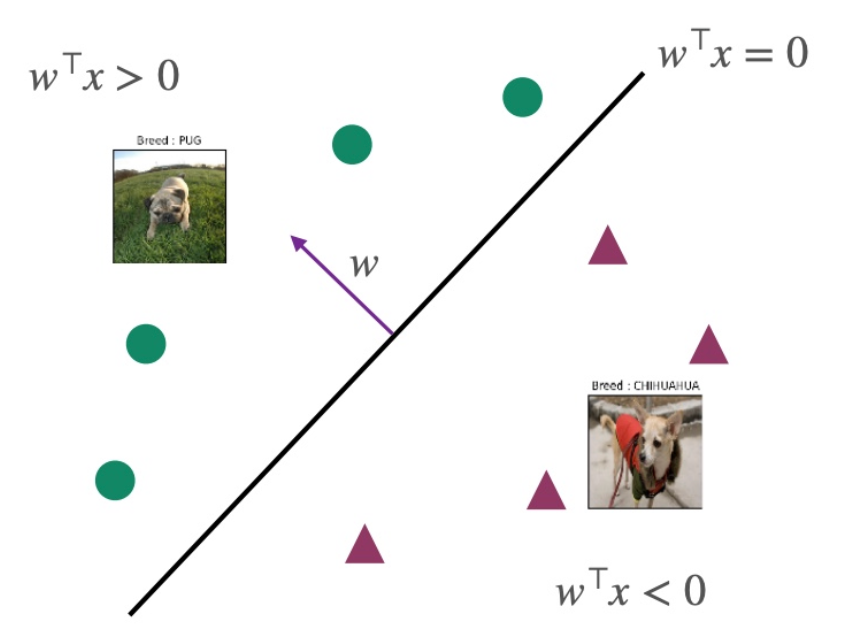
decision boundary

P(y=1∣x)P(y=−1∣x)=1+exp⁡(w⊤x)1+exp⁡(−w⊤x)=exp⁡(w⊤x)\dfrac{P(y=1|x)}{P(y=-1|x)}=\dfrac{1+\exp(w^\top x)}{1+\exp(-w^\top x)}=\exp(w^\top x)的结果表示

如果w⊤x=0w^\top x=0，则P(y=1∣x)=P(y=−1∣x)P(y=1|x)=P(y=-1|x)

如果w⊤x>0w^\top x>0，则P(y=1∣x)>P(y=−1∣x)P(y=1|x)>P(y=-1|x)，label=1的概率更大

如果w⊤x<0w^\top x<0，则P(y=1∣x)<P(y=−1∣x)P(y=1|x)<P(y=-1|x)，label=-1的概率更大

如果w⊤x=0w^\top x=0，则P(y=1∣x)P(y=−1∣x)=exp⁡(w⊤x)\dfrac{P(y=1|x)}{P(y=-1|x)}=\exp(w^\top x)，此时恰好表示处于分界线上，见下图

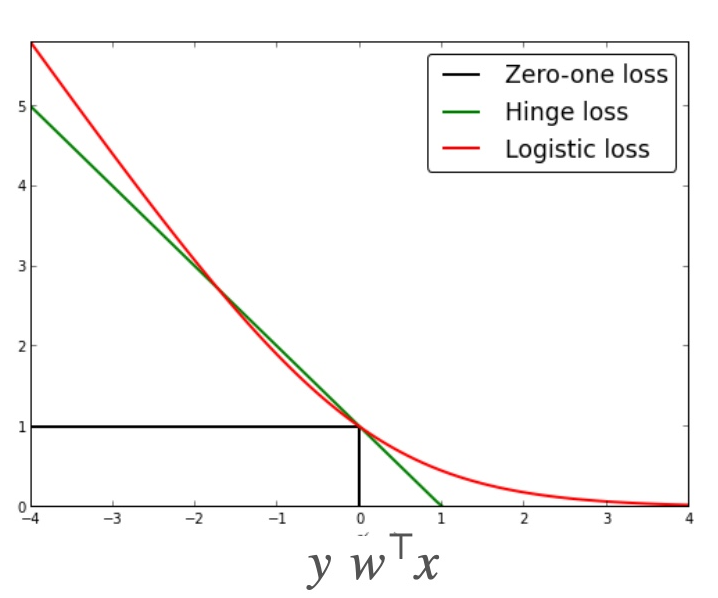
loss function（推导ERM的方法1）

ℓ(f(x),y)={−log⁡(f(x))if y=1−log⁡(1−f(x))otherwise\ell(f(x),y)=\left\{ \begin{aligned} &-\log(f(x)) \qquad &&\text{if}\ y=1\\ &-\log(1-f(x)) \qquad &&\text{otherwise} \end{aligned} \right.

带入f(x) 化简得到log⁡(1+exp⁡(−yωTx))\log(1+\exp(-y\omega^Tx))

注：这是logistic loss，1代表预测错误，0代表预测正确

MAXIMUM LIKELIHOOD ESTIMATOR（推导ERM的方法2）

目的：为了得到最优化的结果，可以和loss function类比，一个是maximum 概率，一个是minimum 误差。

贝叶斯分布，在θ\theta这个参数的情况下，把所有xix_i和yiy_i带入之后的概率的乘积。

L^(θ)=P(S∣θ)=∏i=1mP(xi,yi∣θ)=−∑i=1mlog⁡(1+exp⁡(−yiw⊤xi))\mathscr{\hat L}(\theta)=P(S|\theta)=\prod_{i=1}^mP(x_i,y_i|\theta)\\=-\sum_{i=1}^m\log(1+\exp(-y_iw^\top x_i))

SS是train data。通过上式然后求log，可以推出ERM，具体推导见slides

Empricial Risk Minizer(convex)

R^(w)=1m∑i=1mlog⁡(1+exp⁡(−yiw⊤xi))\hat R(w)=\frac{1}{m}\sum_{i=1}^m \log(1+\exp(-y_i w^\top x_i))

声明：此blog内容为上课笔记，仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权，请联系aursus.blog@gmail.com删除。