K means 聚类
假设
有k个subset C1,C2,C3,...,Ck,有1,...,n个数据点,且所有数据点满足以下条件:
- 每个点都属于一个cluster
- 每个cluster都互不重叠
定义距离
Z(C1,⋯,Ck)=l=1∑k2∣Cl∣1i,j∈Cl∑∥xi−xj∥22
where ∣Ck∣ denotes the number of observations in the kth cluster.
目的是最小化每个cluster的pairwise squared distance
Z(C1,⋯,Ck)=l=1∑ki∈Cl∑k∣∣xi−μl∣∣22
其中,
ul=∣Cl∣1i∈Cl∑xi
迭代目标
minc1,⋯,ckZ(C1,⋯,Ck)
算法|Lloyd’s algorithm

不一定是最优的,因为如果initialize给的点不好的话,会导致结果收敛到一个次优的聚类
- input:x1,x2,...,xk
- initial:C1,C2,...,Ck
- loss function
Z(C1,⋯,Ck)=l=1∑k2∣Cl∣1i,j∈Cl∑∥xi−xj∥22
-
如果还没有converge,
- update centroids
- update clusters
选择一:决定k的大小
如果Zk+1<<Zk,则有必要增加这个k,即k→k+1
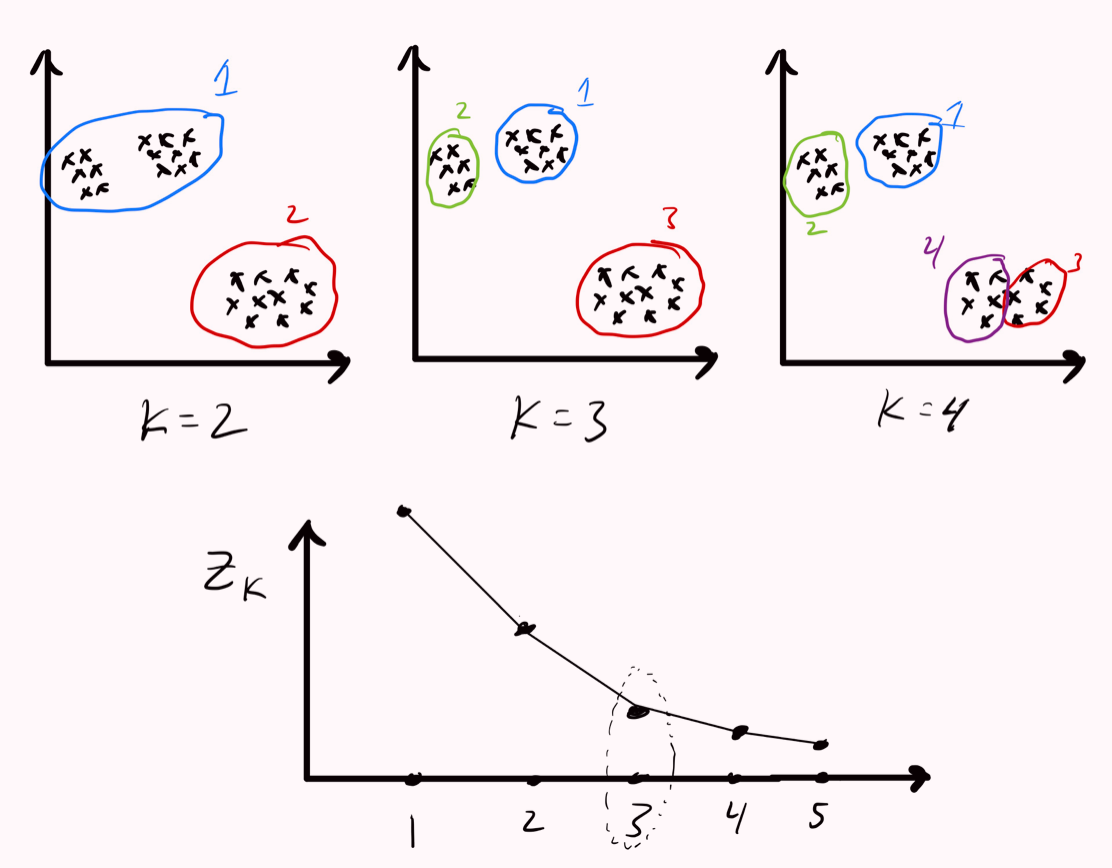
选择二:决定初始聚类分配initial cluster assignment
- 每个人都尝试几个随机的初始聚类分配点,然后从中找到Lloyd’s algorithm下最小的那个结果
- 或者通过k-means ++的方法:随机选择第一个数据点作为中心,然后根据已选中心的距离加权的分布来选择后续的中心
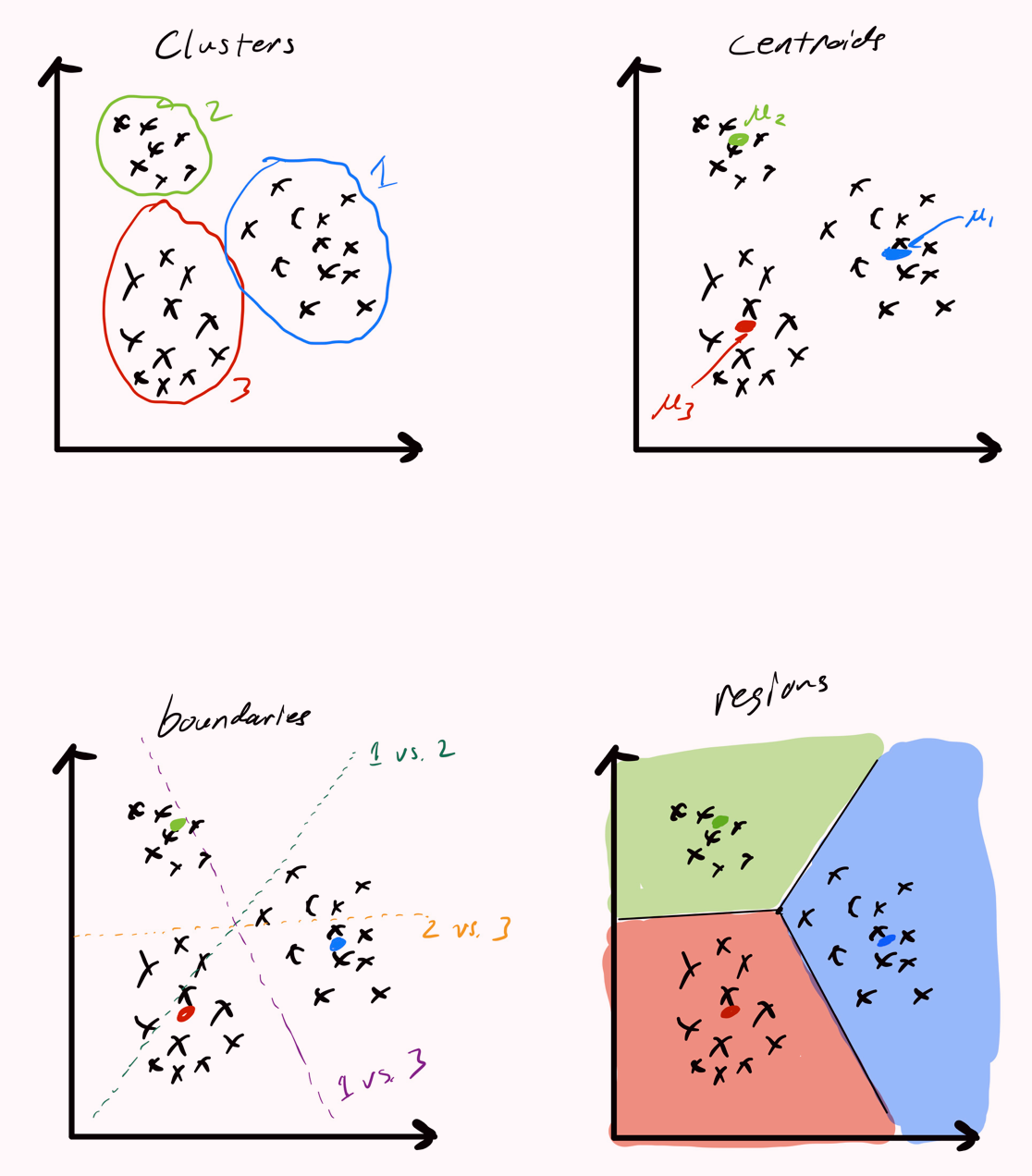
Decision boundaries
通过两个cluster centroids μl, μl′计算{x∈Rd ∣ ∣∣x−μl∣∣2=∣∣x−μl′∣∣2}可以计算得到
参考资料
https://www.cs.cornell.edu/courses/cs4780/2022sp/notes/LectureNotes04.html
声明:此blog内容为上课笔记,仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权,请联系aursus.blog@gmail.com删除。


