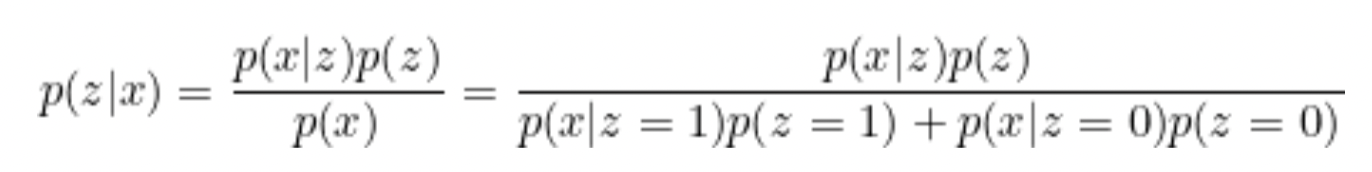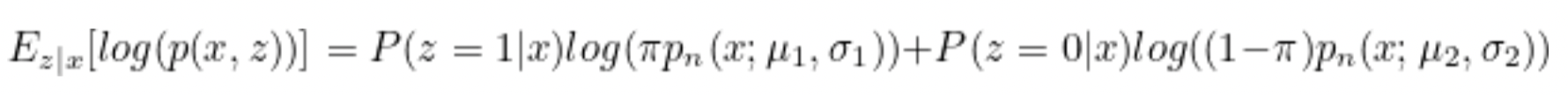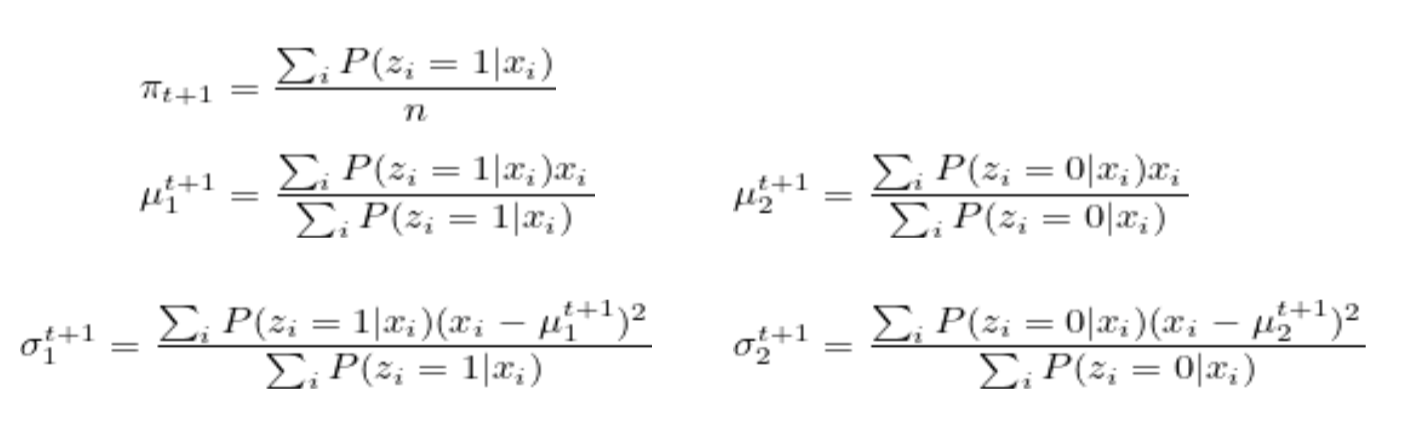生物医学工程 | 机器学习 - Gaussian Mixture & EM

GMM（Gaussian Mixture Model）

什么是高斯混合模型？

首先我们有k个高斯模型，他们分别为$ N(\mu_1, \sigma_1^2), N(\mu_2, \sigma_2^2), …, N(\mu_k, \sigma_k^2) $

我们按照一定的比例从$N(\mu_j, \sigma_j^2)$这个高斯函数中取了比例为$\phi_j$的一些样本。

按照经验可得，$\sum_{j=1}^{k}\phi_j=1$，即所有比例之和为1。

$p(z^{(i)}=j)=\phi_j$表示在$z=j$这个cluster的概率，如果是hard assignment，则用$\mathbb{I}({z^{(i)}=j})$表示。如果在这个cluster，即则$z^{(i)}=j$，则概率为1，反之不在这个cluster则为0。

$p(x^{(i)}|z^{(i)}=j)=p_{norm}(x^{(i)};\mu_j,\sigma_j)$表示在$j$这个高斯分布中的取到$x$的概率，如

每一个$x^{(i)}$都对应k个$z^{(i)}_j$

基本参数和分布

input: $$ {x^{(1)}, …, x^{(n)}} $$

latent variable:

$\{z^{(1)}, ..., z^{(n)}\},\ z^{(i)}=(z^{(i)}=1,z^{(i)}=2,...,z^{(i)}=k)$

换而言之，每个$z^{(i)}$都对应一个$x^{(i)}$，$z^{(i)}$满足多项式分布，且可以拆分为分属不同k的z。通过分属不同k的z来拼凑出大的z，从而得到x。

joint distribution

$p(x^{(i)}, z^{(i)})=p(x^{(i)}|z^{(i)})p(z^{(i)})$

其中，$z{(i)}$~ Multinomial$(\phi)$多项式分布，where $\phi_j \geq 0$，$\sum_{j=1}^{k}\phi_j=1$。

$x^{(i)}|z^{(i)}=j\sim N(\mu_j, \Sigma_j)$

$z^{(i)}$指示了每个$x^{(i)}$是从那个k Gaussians来的。

$p(z)$表示probability of choose cluster z，也就是density of mixture model

$p(z^{(i)}=j)$表示在z=j这个cluster的概率

i表示第几个data的index，x表示data

j表示第几个cluster的index，z表示cluster

参数$\phi_j$提供$p(z^{(i)}=j)$，$x^{(i)}|z^{(i)}=j\sim N(\mu_j, \Sigma_j)$，即x|z满足某一个高斯分布，N（）为高斯分布

likelihood of data

$\ell(\phi, \mu, \Sigma) = \sum_{i=1}^{n}\log p(x^{(i)};\phi, \mu, \Sigma) ---(1)\\ = \sum_{i=1}^{n}\log\sum_{z^{(i)}=1}^{k}p(x^{(i)}|z^{(i)}=j; \mu,\Sigma)p(z^{(i)}=j;\phi)---(2)\\$

为了解决（1），所以我们引入了z从而将这一个概率拆为两个部分的概率的相乘，从而得到（2）

其中;左侧表示变量，右侧表示参数，,表示并列。$x|z;\mu,\Sigma$中，$｜$的右侧表示整体范围（即$z=j$的范围内），左侧$x$表示在右侧那些范围中x的概率

如果$z^{(i)}$已知的话，即如果我们知道zi来自于哪个高斯分布，换句话说我们把j固定了下来，则式子可以化简为

$\ell(\phi, \mu, \Sigma) = \sum_{i=1}^{n}\log p(x^{(i)}|z^{(i)}; \mu,\Sigma)+\log p(z^{(i)};\phi)---(3)$

maximum函数（3），通过求偏导=0，从而算出结果为：（此时固定了j）

$\phi _ { j } = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } 1 \{ z ^ { ( i ) } = j \}$

$\mu _ { j } = \frac { \sum _ { i = 1 } ^ { n } 1 \{ z ^ { ( i ) } = j \} x ^ { ( i ) } } { \sum _ { i = 1 } ^ { n } 1 \{ z ^ { ( i ) } = j \} }$

$\Sigma _ { j } = \frac { \sum _ { i = 1 } ^ { n } 1 \{ z ^ { ( i ) } = j \} ( x ^ { ( i ) } - \mu _ { j } ) ( x ^ { ( i ) } - \mu _ { j } ) ^ { T } } { \sum _ { i = 1 } ^ { n } 1 \{ z ^ { ( i ) } = j \} }$

从上图可以看出来，$z^{(i)}$可以视为class label的作用，所以只要知道$z^{(i)}$就可以都求出来了，所以我们通过使用EM方法来求$z^{(i)}$

EM (Expectation-Maximization) algorithm for density estimation

（E-Step） 猜测$z^{(i)}$，cluster assignment

For each $i, j$, set

$w _ { j } ^ { ( i ) } : = p ( z ^ { ( i ) } = j | x ^ { ( i ) } ; \phi , \mu , \Sigma )$

这个$\omega_j^{(i)}$表示我们对$z^{(i)}$的猜测。因为我们要求z，所以把z放在｜的左边

通过Bayes 法则，我们可以得到：

$p(z|x)=\frac{p(x|z)p(z)}{p(x)}$

$p ( z ^ { ( i ) } = j | x ^ { ( i ) } ; \phi , \mu , \Sigma ) = \frac { p ( x ^ { ( i ) } | z ^ { ( i ) } = j ; \mu, \Sigma ) p ( z ^ { ( i ) } = j ; \mu, \Sigma ) p ( z ^ { ( i ) } = j ; \phi ) } { \sum _ { l = 1 } ^ { k } p ( x ^ { ( i ) } | z ^ { ( i ) } = l ; \mu, \Sigma ) p ( z ^ { ( i ) } = l ; \phi )}$

$f(x)=\frac{1}{\sqrt{(2\pi)^k \det \Sigma}} \exp (-\frac{1}{2}(x-\mu)^{T}\Sigma ^{-1}(x-\mu))$

$p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)$来自于density of Gaussian with mean $\mu_j$和convariance$\Sigma_j$，表示如果xi来自于高斯分布j，则从该模型中取到x的概率

$p(z^{(i)}=j;\phi)$=$\phi_j$，表示来自于j这个高斯模型的概率

（M-Step） 基于猜测update model的parameter（MLE）——soft assignment

Update the parameters:

$\phi _ { j } : = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } w _ { j } ^ { ( i ) }$

$\mu _ { j } : = \frac { \sum _ { i = 1 } ^ { n } w _ { j } ^ { ( i ) } x ^ { ( i ) } } { \sum _ { i = 1 } ^ { n } w _ { j } ^ { ( i ) } }$

$\Sigma _ { j } : = \frac { \sum _ { i = 1 } ^ { n } w _ { j } ^ { ( i ) } ( x ^ { ( i ) } - \mu _ { j } ) ( x ^ { ( i ) } - \mu _ { j } ) ^ { T } } { \sum _ { i = 1 } ^ { n } w_j ^{(i)} }$

Restriction

$\Sigma_j=\sigma^2I$

其中$\sigma^2\rightarrow 0$则原函数化简为k-means

从概率的角度而言，高斯图像无限逼近脉冲函数，只有靠近中心的位置才有数值，其余都很小。因此针对于某一个高斯分布，概率很大，对其他而言，概率很小。所以从w的数值而言，按照贝叶斯分布的那个分子分母公式，这个数据只有在某一个高斯分布里面才会很大，其他都无限接近于0.

从cluster的角度而言，sigma变为0表示GMM椭圆的cluster边界变为k-mean圆形的边界（或者说椭球形变为球型）

K-means的进阶方法

不再使用hard cluster assignment $c(i)$，而是使用soft assignments $\omega_j^{(i)}$

作业代码里面，w是mxk的矩阵，里面装着xi属于高斯分布j的概率。如果要变成hard cluster，只要遍历xi在所有k个高斯分布里面概率，找到最大概率的那个高斯分布，然后就认定是这个高斯分布，除此以外的概率都是0，所以矩阵退化为mx1的向量。

GMM求解

GMM可以通过run EM或者min loss function来求解

其他

从cluster l中观测到x的概率：

$P(x) = \sum P(x, z=l) = \sum P(x|z=l)P(z=l)$

单个参数，用求导

多个参数，用MLE或者EM

reference

https://mas-dse.github.io/DSE210/Additional Materials/gmm.pdf

什么是高斯混合模型

https://www.bilibili.com/video/BV12d4y167ud/?spm_id_from=333.337.search-card.all.click

https://www.bilibili.com/video/BV1Dd4y167pZ/?spm_id_from=333.788.recommend_more_video.-1&vd_source=2029748cdca0ccea25511170cf7a00c3

---

两个高斯模型组成的，选到模型1的概率为 $\pi$，选到模型2的概率为 $1-\pi$。下面就是选到了x模型的概率

$p ( x ; \pi , \sigma _ { 1 } , \sigma _ { 2 } , \mu _ { 1 } , \mu _ { 2 } ) = \pi p _ { n o r m } ( x ; \mu _ { 1 } , \sigma _ { 1 } ) + ( 1 - \pi ) p _ { n o r m } ( x ; \mu _ { 2 } , \sigma _ { 2 } )$

对其进行 $log$，因为 $log(x)$ 是函数，所以求 $\max x$ 和求 $\max \log(x)$ 一个道理

$\log ( L ( x ; \pi , \mu _ { 1 } , \mu _ { 2 } , \sigma _ { 1 } , \sigma _ { 2 } ) ) = \sum \log ( \pi p _ { n o r m } ( x ; \mu _ { 1 } , \sigma _ { 1 } ) + ( 1 - \pi ) p _ { n o r m } ( x ; \mu _ { 2 }, \sigma_2 ) )$

$p ( x , z ) = p ( x | z ) p ( z )$

where,

$z \in \{ 0 , 1 \} , p ( z = 1 ) = \pi ,\\ p ( x | z = 1 ) = p _ {norm} ( x ; \mu _ { 1 } \sigma_1),\\ p ( x | z =0 ) = p _ {norm}(x; \mu_2, \sigma_2)$

z和x同时发生的概率=z发生的概率*x发生的概率然后求和

${ \log ( L ( p ( z , x ; \pi , \mu _ { 1 } , \mu _ { 2 } , \sigma_1, \sigma _ { 2 } ) ) ) } \\ { = \sum _ { i } z _ { i } \log ( \pi p _ { n } ( x _ { i } ; \mu _ { 1 } , \sigma _ { 1 } )) + ( 1 - z _ { i } ) \log ( ( 1 - \pi ) p_n (x_i; \mu_2,\sigma_2))}$

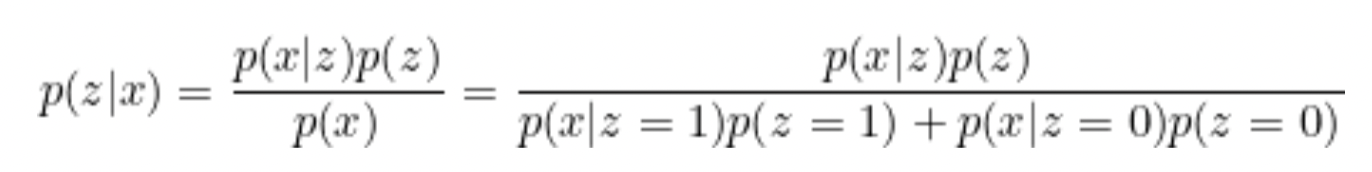
期望=log（p（x，z））的概率乘以是否发生，也就是p（z=1｜x）

---

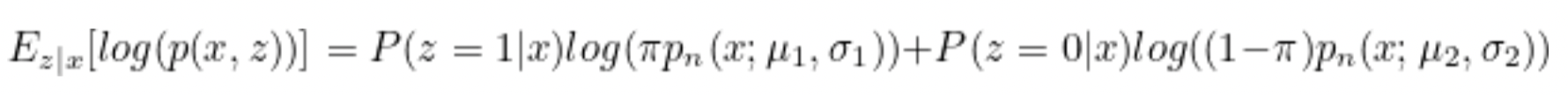
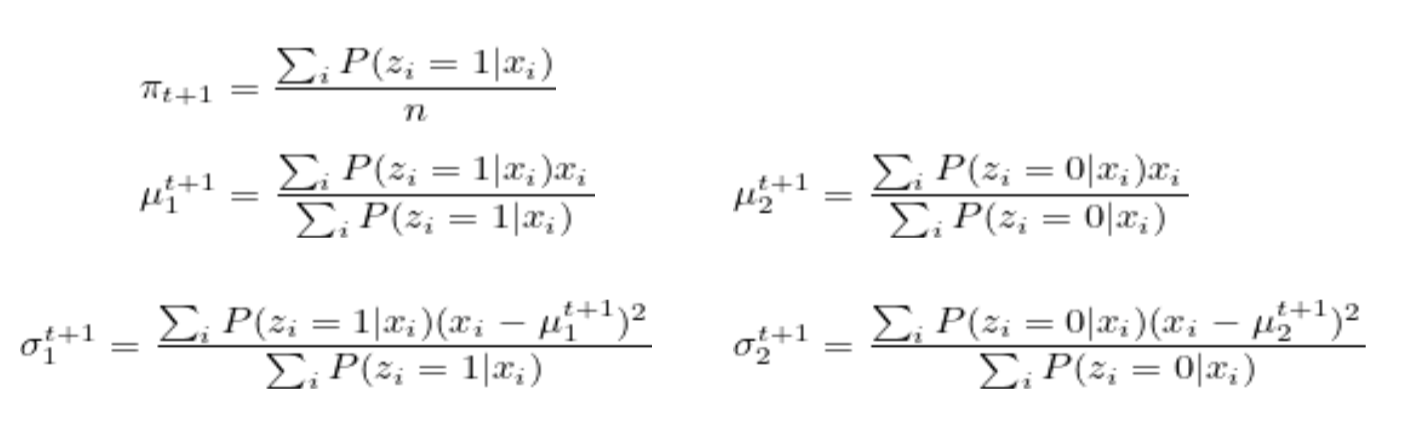
声明：此blog内容为上课笔记，仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权，请联系aursus.blog@gmail.com删除。