Logistic Regression

Utilization: Curve fitting, classification into two classes, typically deals with data points.

Applicability: Can be applied universally. If data separation can be achieved with a single line, logistic regression can be used.

Input Space

X=Rd\mathcal{X}=\mathbb{R}^d

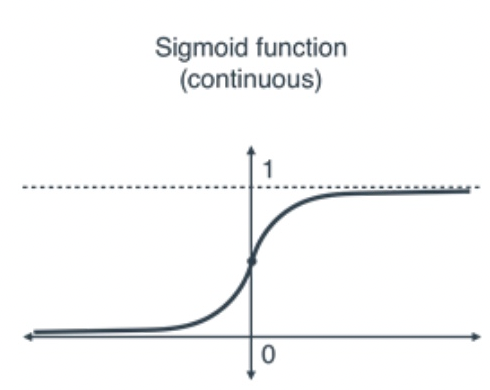
Label Space/Output Space (y ranges from 0 to 1)

Y=[0,1]\mathcal{Y}=[0,1]

Hypothesis Class FF

F:={x↦sigmoid(w⊤x+b) ∣ w∈Rd,b∈R},where sigmoid(a)=11+exp⁡(−a)\mathcal{F}:=\{x \mapsto \text{sigmoid}(w^\top x+b)\ |\ w\in\mathbb{R}^d, b\in\mathbb{R}\}, \text{where } \text{sigmoid}(a)=\frac{1}{1+\exp(-a)}

Note: ω\omega: weight vector; bb: bias

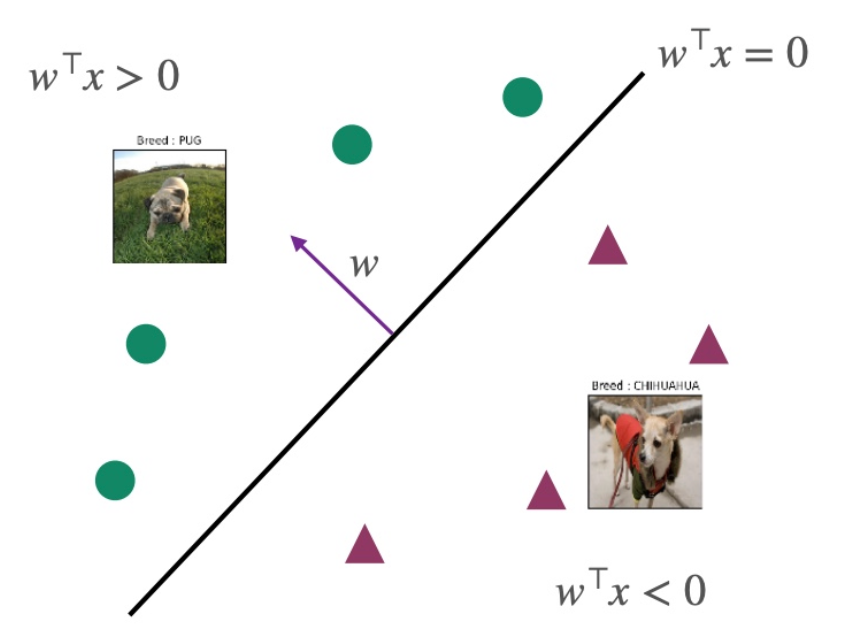
Decision Boundary

The result of P(y=1∣x)P(y=−1∣x)=1+exp⁡(w⊤x)1+exp⁡(−w⊤x)=exp⁡(w⊤x)\dfrac{P(y=1|x)}{P(y=-1|x)}=\dfrac{1+\exp(w^\top x)}{1+\exp(-w^\top x)}=\exp(w^\top x) indicates:

  • If w⊤x=0w^\top x=0, then P(y=1∣x)=P(y=−1∣x)P(y=1|x)=P(y=-1|x).
  • If w⊤x>0w^\top x>0, then P(y=1∣x)>P(y=−1∣x)P(y=1|x)>P(y=-1|x), indicating a higher probability for label=1.
  • If w⊤x<0w^\top x<0, then P(y=1∣x)<P(y=−1∣x)P(y=1|x)<P(y=-1|x), indicating a higher probability for label=-1.
  • If w⊤x=0w^\top x=0, then P(y=1∣x)P(y=−1∣x)=exp⁡(w⊤x)\dfrac{P(y=1|x)}{P(y=-1|x)}=\exp(w^\top x), precisely at the decision boundary.

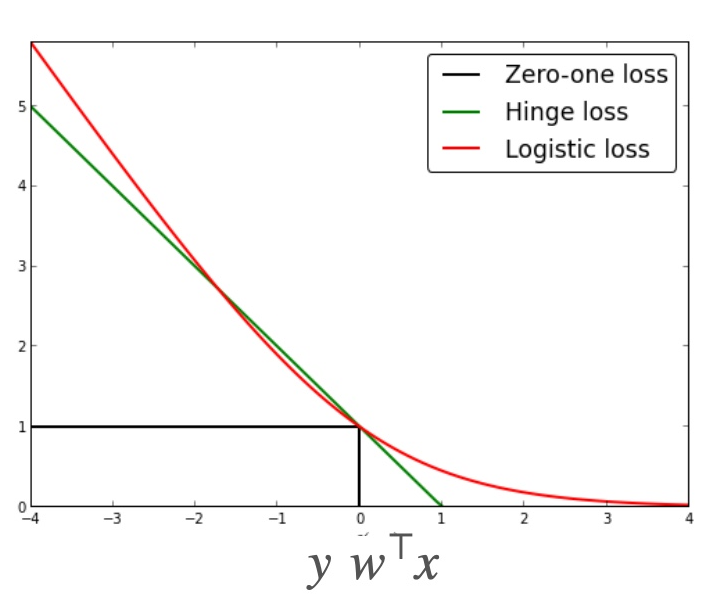
Loss Function (Derivation of ERM - Method 1)

ℓ(f(x),y)={−log⁡(f(x))if y=1−log⁡(1−f(x))otherwise\ell(f(x),y)=\left\{ \begin{aligned} &-\log(f(x)) \qquad &&\text{if}\ y=1\\ &-\log(1-f(x)) \qquad &&\text{otherwise} \end{aligned} \right.

Substituting f(x)f(x) and simplifying yields log⁡(1+exp⁡(−yωTx))\log(1+\exp(-y\omega^Tx)).

Note: This is the logistic loss, where 1 represents a wrong prediction and 0 indicates a correct prediction.

MAXIMUM LIKELIHOOD ESTIMATOR (Derivation of ERM - Method 2)

Objective: To achieve optimal results, it can be compared to the loss function where one maximizes probability and the other minimizes error.

Bayesian distribution, the product of probabilities of all xix_i and yiy_i given the parameter θ\theta.

L^(θ)=P(S∣θ)=∏i=1mP(xi,yi∣θ)=−∑i=1mlog⁡(1+exp⁡(−yiw⊤xi))\mathscr{\hat L}(\theta)=P(S|\theta)=\prod_{i=1}^m P(x_i,y_i|\theta)\\=-\sum_{i=1}^m \log(1+\exp(-y_iw^\top x_i))

SS represents the train data. ERM can be derived from the above equation by taking its logarithm. For specific derivation steps, refer to the slides.

Empirical Risk Minimizer (Convex)

R^(w)=1m∑i=1mlog⁡(1+exp⁡(−yiw⊤xi))\hat R(w)=\frac{1}{m}\sum_{i=1}^m \log(1+\exp(-y_i w^\top x_i))

Disclaimer: This blog content is intended as class notes and is solely for sharing purposes. Some images and content are sourced from textbooks, teacher presentations, and the internet. If there are any copyright infringements, please contact aursus.blog@gmail.com for removal.