Binary Classification

Assumptions

  1. Linearly separable data.
  2. Binary classification, meaning the data can be divided into two classes.

Objective

To categorize the data into two classes based on labels.

Set up

Input space

X=Rd\mathcal{X} = \mathbb{R}^d

Label space / Output space

Y={−1,1}\mathcal{Y} = \{-1, 1\}

Classifier | Hypothesis class F\mathcal{F}

F:={x↦sign(w⊤x+b) ∣ w∈Rd,b∈R}\mathcal{F} := \{x \mapsto \text{sign}(\mathbf{w}^\top \mathbf{x} + \mathbf{b})\ |\ \mathbf{w}\in\mathbb{R}^d,\mathbf{b}\in\mathbb{R}\}

Where ω\omega is the weight vector; bb is the bias, and sign is the sign function defined as:

sign(a)={1if a≥0−1otherwise\text{sign}(a)=\left\{ \begin{aligned} &1 \qquad &&\text{if}\ a\geq0\\ &-1 \qquad &&\text{otherwise} \end{aligned} \right.

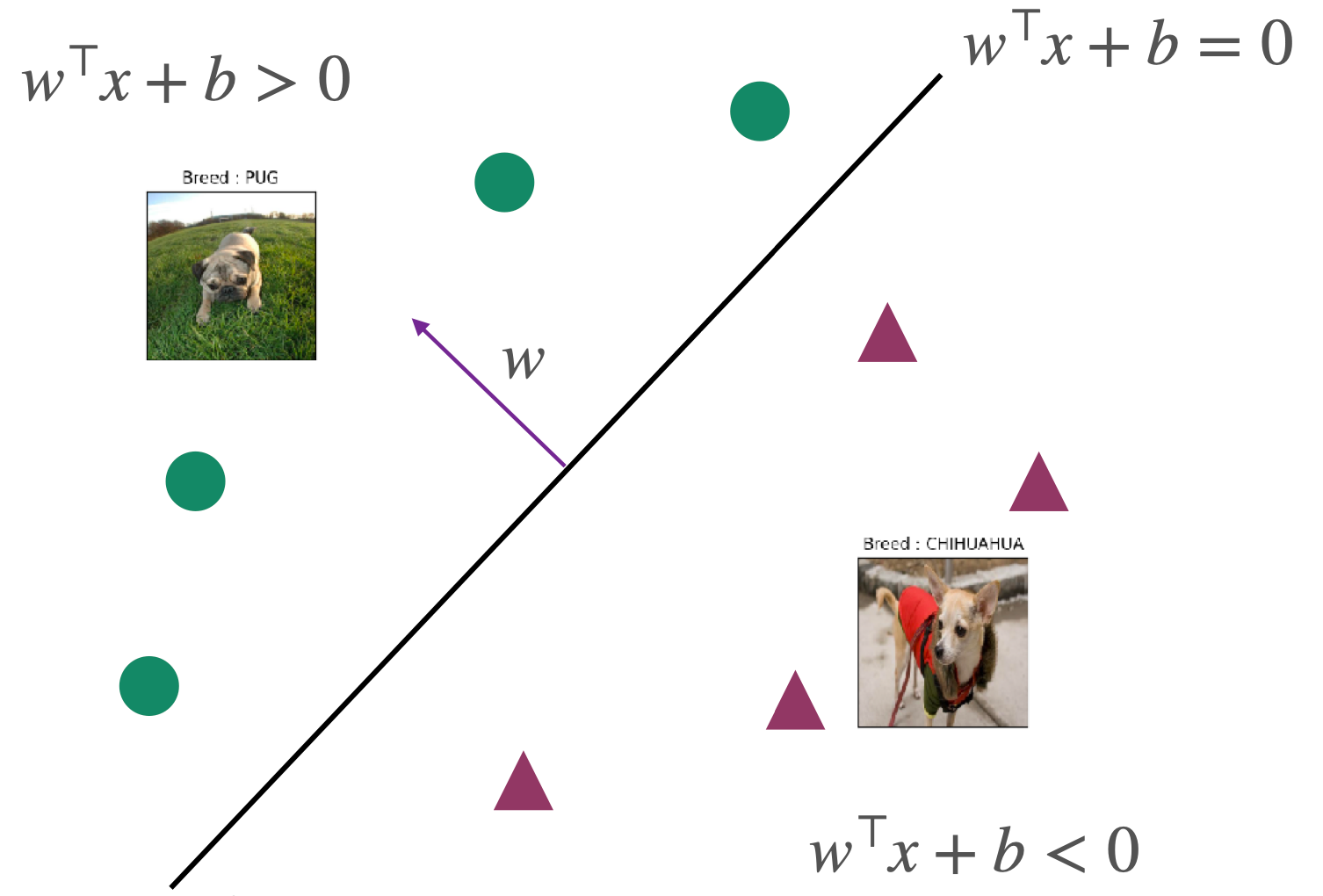
To simplify subsequent calculations, we aim to have the classifier containing only ww without bb. For this purpose, we add a dimension and treat bb in the second dimension of ww as a constant, as follows:

x↦[x1]w↦[wb]x \mapsto \left[ \begin{matrix}x\\1 \end{matrix}\right] \quad w \mapsto \left[ \begin{matrix}w\\b \end{matrix}\right]

The original classifier simplifies to

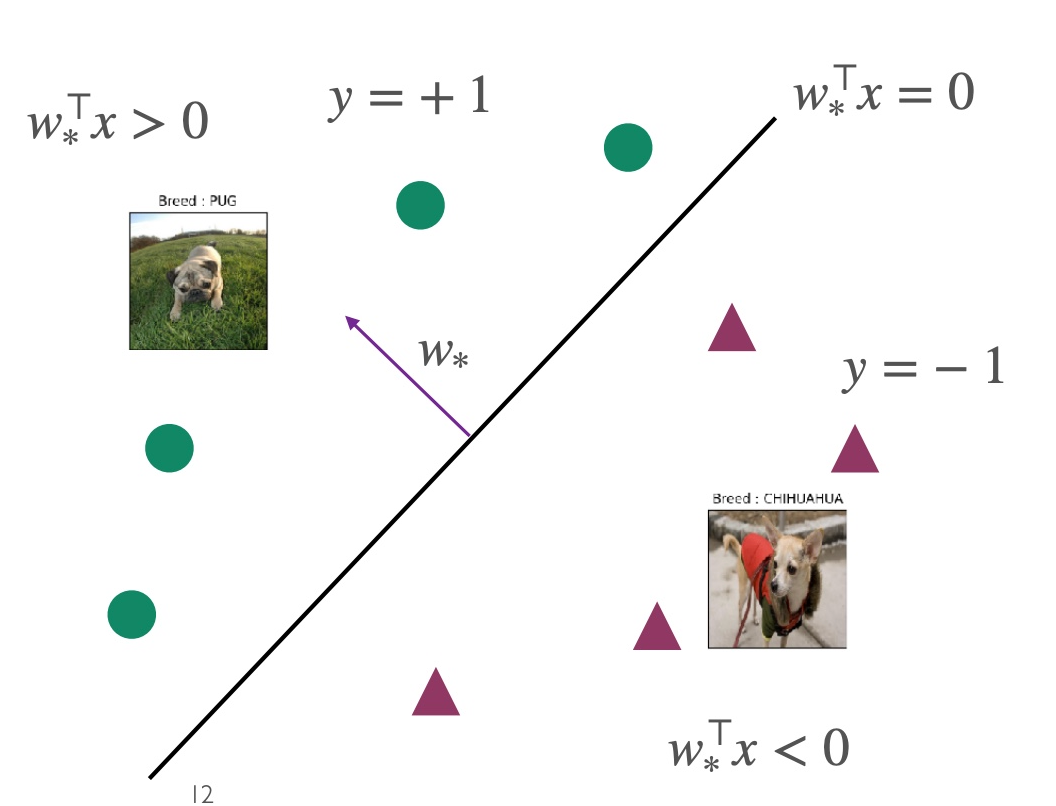
F:={x↦sign(w⊤x) }\mathcal{F} := \{x \mapsto \text{sign}(\mathbf{w}^\top \mathbf{x})\ \}

Empirical Risk Minimizer

We use the following loss function to find ERM:

ℓ(f(x),y)={0if f(x)=y1otherwise\ell(f(x),y)=\left\{ \begin{aligned} &0 \qquad &&\text{if}\ f(x)=y\\ &1 \qquad &&\text{otherwise} \end{aligned} \right.

This expression is also known as 0-1 loss, where 1 represents prediction error, and 0 represents correct prediction. This expression can also be represented using the indicator function I\mathbb{I} (Indicator function) as:

I[f(x)≠y]={1if f(x)≠y0if f(x)=y\mathbb{I}[f(x)\neq y] = \left\{ \begin{aligned} &1 \qquad &&\text{if}\ f(x)\neq y\\ &0 \qquad &&\text{if}\ f(x)= y \end{aligned} \right.

By substituting the classifier into the loss function, we can derive ERM as follows:

min⁡werr^(w)=min⁡w1m∑i=1mI[sign(w⊤xi)≠yi]=min⁡w1m∑i=1mI[sign(yiw⊤xi<0)]\begin{aligned} \min_w \hat{err}(w)&=\min_w \frac{1}{m}\sum_{i=1}^m \mathbb{I}[\text{sign}(w^\top x_i)\neq y_i]\\ &= \min_w \frac{1}{m}\sum_{i=1}^m \mathbb{I}[\text{sign}(y_iw^\top x_i<0)] \end{aligned}

The ww that minimizes ERM is denoted as w^\hat w:

w^=arg⁡min⁡w1m∑i=1mI[sign(w⊤xi)≠yi]=arg⁡min⁡w1m∑i=1mI[sign(yiw⊤xi<0)]\begin{aligned} \hat w&=\arg\min_w \frac{1}{m}\sum_{i=1}^m \mathbb{I}[\text{sign}(w^\top x_i)\neq y_i]\\ &=\arg \min_w \frac{1}{m}\sum_{i=1}^m \mathbb{I}[\text{sign}(y_iw^\top x_i<0)] \end{aligned}

In the case of linearly separable data, w^\hat w is referred to as w∗w^*. At this point, w∗w^* satisfies yi=sign(ω∗⊤xi)y_i=sign(\omega_*^\top x_i) for any point, and ω∗⊤xi\omega_*^\top x_i serves as the boundary between the two categories.

Perceptron Algorithm

Objective

Update ww until all data points are correctly classified.

Applicability

  1. Data points must be completely linearly separable.
  2. Once data like XOR or non-linearly separable data occurs, the perceptron cannot be used.
    1. XOR and non-linearly separable data can be segmented using kernel SVM.

Algorithm

Update Rule

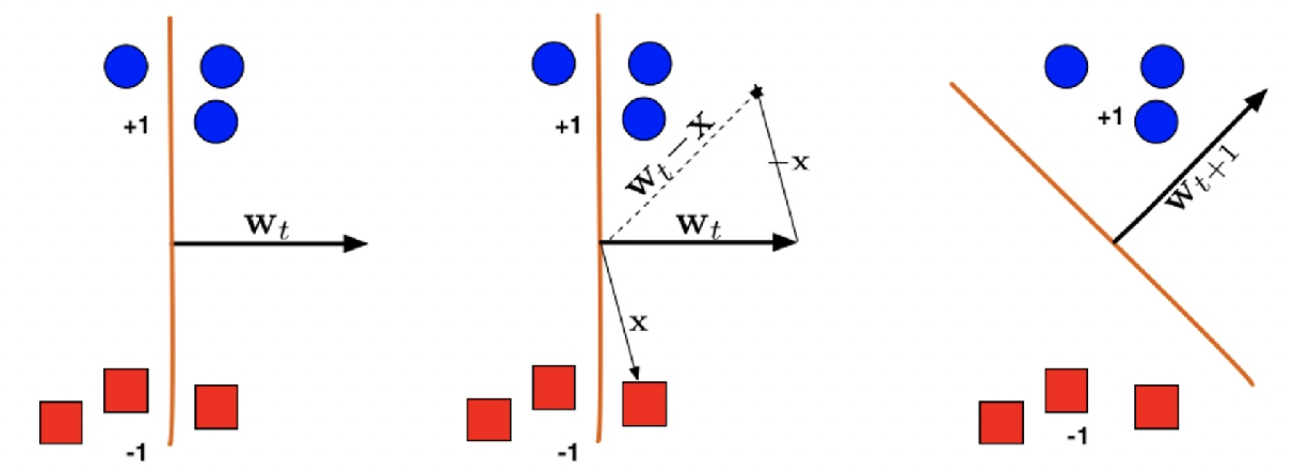
If misclassified, i.e., sign(w⊤xi)≠yi\text{sign}(w^\top x_i)\neq y_i or sign(yiw⊤xi<0)\text{sign}(y_iw^\top x_i<0), update according to rule wt+1=wt+yixiw_{t+1}=w_t+y_ix_i.

If yi=1y_i=1, then wt+1⊤xi=wt⊤xi+∥xi∥2>wt⊤xiw_{t+1}^\top x_i = w_t^\top x_i +\|x_i\|^2 > w_t^\top x_i. w updates towards the positive direction.

If yi=−1y_i=-1, then wt+1⊤xi=wt⊤xi−∥xi∥2<wt⊤xiw_{t+1}^\top x_i = w_t^\top x_i -\|x_i\|^2 < w_t^\top x_i. w updates towards the negative direction.

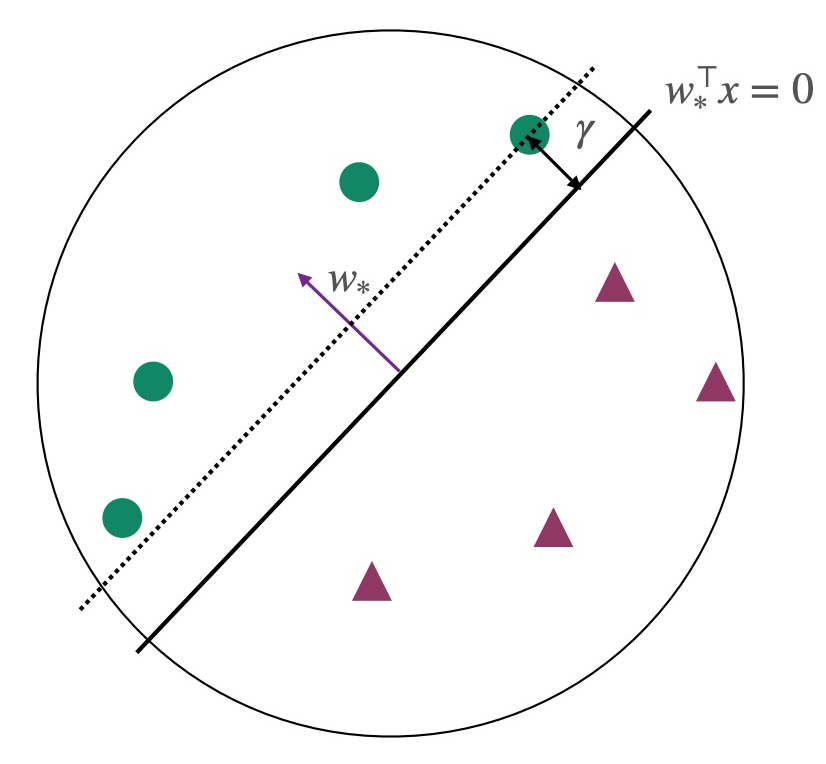
Margin γ\gamma and Convergence of the Algorithm

Assumptions: All points lie within the unit circle ∣∣xi∣∣2≤1||x_i||_2≤1, and at this point ∣∣ω∗∣∣=1||\omega_*||=1.

Conclusion: The Perceptron algorithm converges in at most 1/γ21/\gamma^2 rounds, returning a classifier where sign(ωTxi)=yi\text{sign}(\omega^Tx_i)=y_i. At this stage, all points are correctly classified.

Proof: Refer to https://machine-learning-upenn.github.io/assets/notes/Lec2.pdf

Margin γ\gamma: Represents the minimum distance of all points to the hyperplane.

γ=min⁡i∈[m]∣w∗⊤xi∣∥w∥=min⁡i∈[m]∣w∗⊤xi∣\gamma=\min_{i\in[m]}\frac{|w_*^\top x_i|}{\|w\|}=\min_{i\in[m]}|w_*^\top x_i|

References:

https://www.cs.cornell.edu/courses/cs4780/2022sp/notes/LectureNotes06.html

https://machine-learning-upenn.github.io/calendar/

Declaration: The content of this blog is class notes and is for sharing purposes only. Some images and content are sourced from textbooks, lecture materials, and the internet. If there is any infringement, please contact aursus.blog@gmail.com for removal.