基本概念：小波变换就是用一组不同频率的short kernel（wavelet）和原始信号进行卷积，因此信号只需要在wavelet的长度上稳定（stationary）

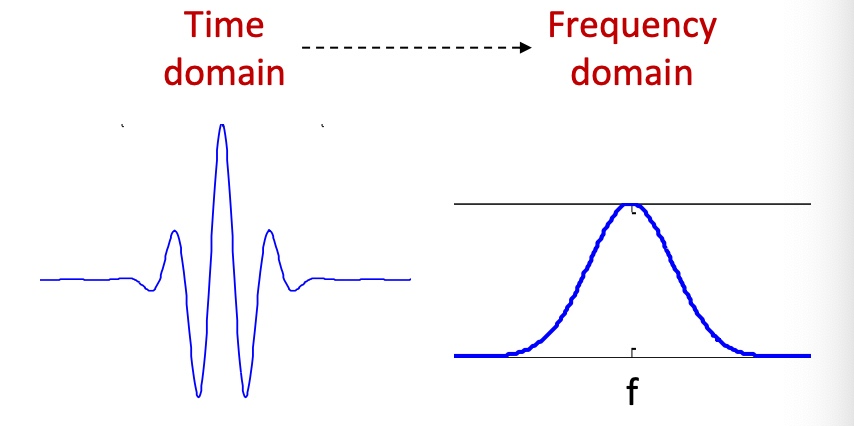
和傅立叶变换相似的是，如果信号的频率和小波的频率接近，则点乘（dot product）得到的结果幅值越大

小波卷积可以当作带通滤波器（band-pass filter）使用。

卷积核

Wavelet的类型

小波变换的卷积核（wavelet）有很多种类型，不同的类型会影响时间分辨率（temporal precision）。通常我们使用最多的是高斯核（Morlet Wavelet）

Wavelet的种类：https://www.mathworks.com/help/wavelet/gs/introduction-to-the-wavelet-families.html

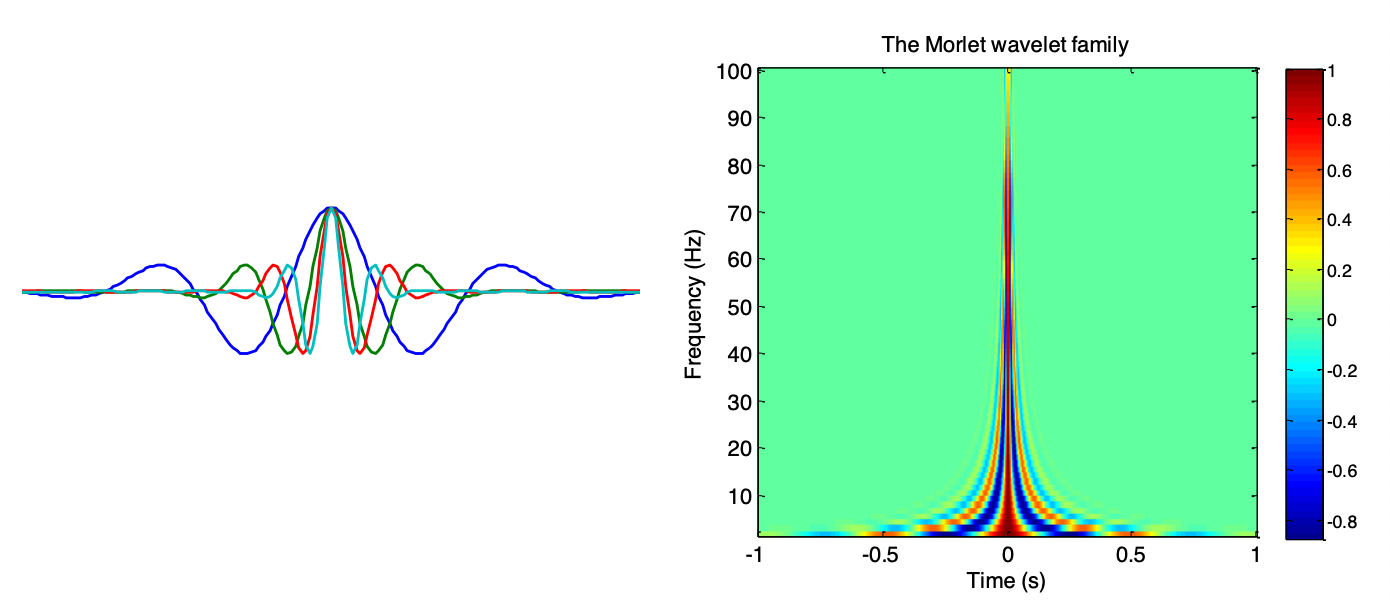
小波族Wavelet Family

定义：我们将同一种类型，但不同频率的一组小波叫做family

Morlet Wavelet Family

Morlet wavelet在时域上表现为外部为高斯函数的包络面，内部为正弦函数。而在频域上则表现为高斯函数，且峰值在wavelet 的频率f上。

Real-valued Morlet Wavelet

数学公式：

asin⁡2πft∗ae−t2/(2s2)a\sin 2\pi ft * a e^{-t^2/(2s^2)}

Q：如何构建Morlet wavelet？

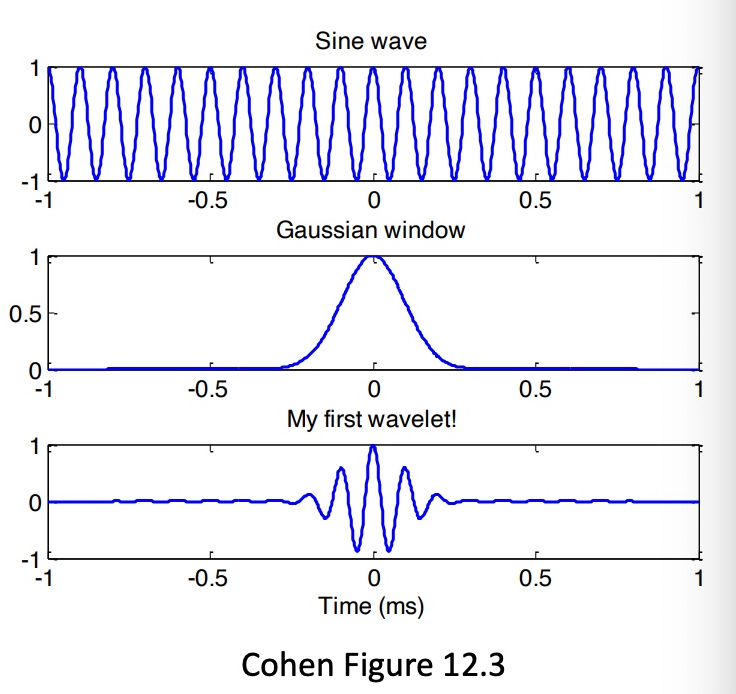
构建一个正弦波（sine wave），并和Gaussian window相乘，得到Morlet wavelet。需要注意的是，Gaussian window和sine wave的采样频率（sampling frequency）和点的数量。

Q：具体的公式是什么呢？

正弦波公式：asin⁡2πfta\sin 2\pi ft

Gaussian公式：ae−t2/(2s2)a e^{-t^2/(2s^2)} where s=n2πfs=\frac{n}{2\pi f}

Wavelet公式：asin⁡2πft∗ae−t2/(2s2)a\sin 2\pi ft * a e^{-t^2/(2s^2)}

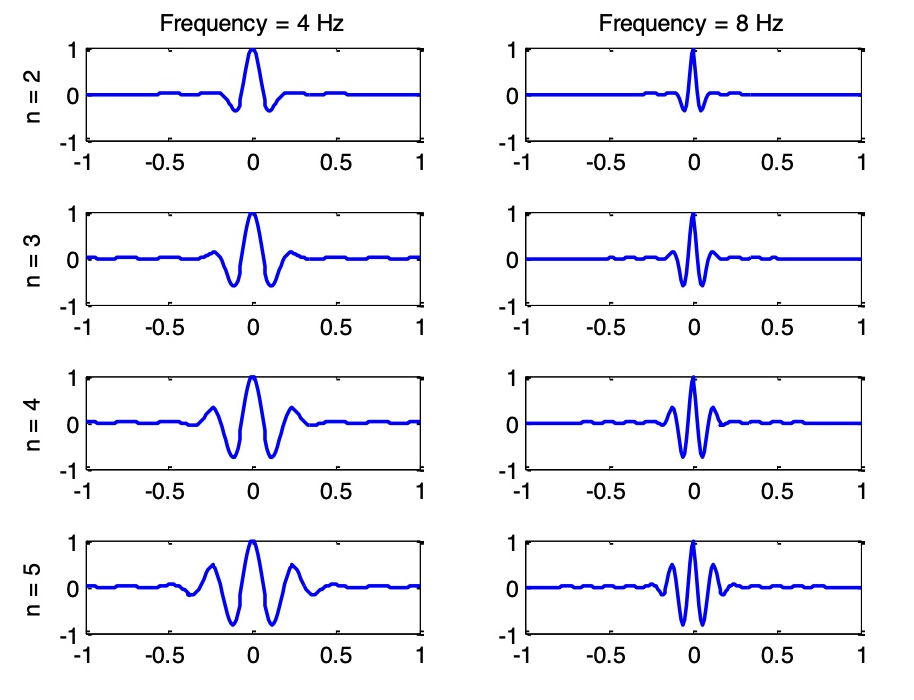
n是wavelet cycles，表示temporal precision和frequency precision的折中（trade-off），f是wavelet的频率。

Q：应该如何选择频率和cycle呢？

最低频率：理论下限为1倍的epoch对应频率，但通常选择4倍的epoch对应频率。如1s的epoch，起码选择4Hz作为wavelet frequency

最高频率：理论上限为奈奎斯特频率（Nyquist frequency），但通常保证每个cycle里面有四个采样点。如500Hz的采样频率，最多选择125Hz作为wavelet frequency

wavelet family数量：一般选择20-30个不同的频率。如EEG的cognitive task我们通常选择4-60Hz。

Q：real-valued wavelet存在什么问题吗？

和傅立叶变换一样，纯实数构成的卷积核要求原始信号和卷积核的相位（phase）相同。因此我们引入complex-valued wavelet

代码

！练习

假设我有一个60s长的采样频率为100Hz的信号，我想要进行wavelet convolution，则代码应该如何编写？

Maltab

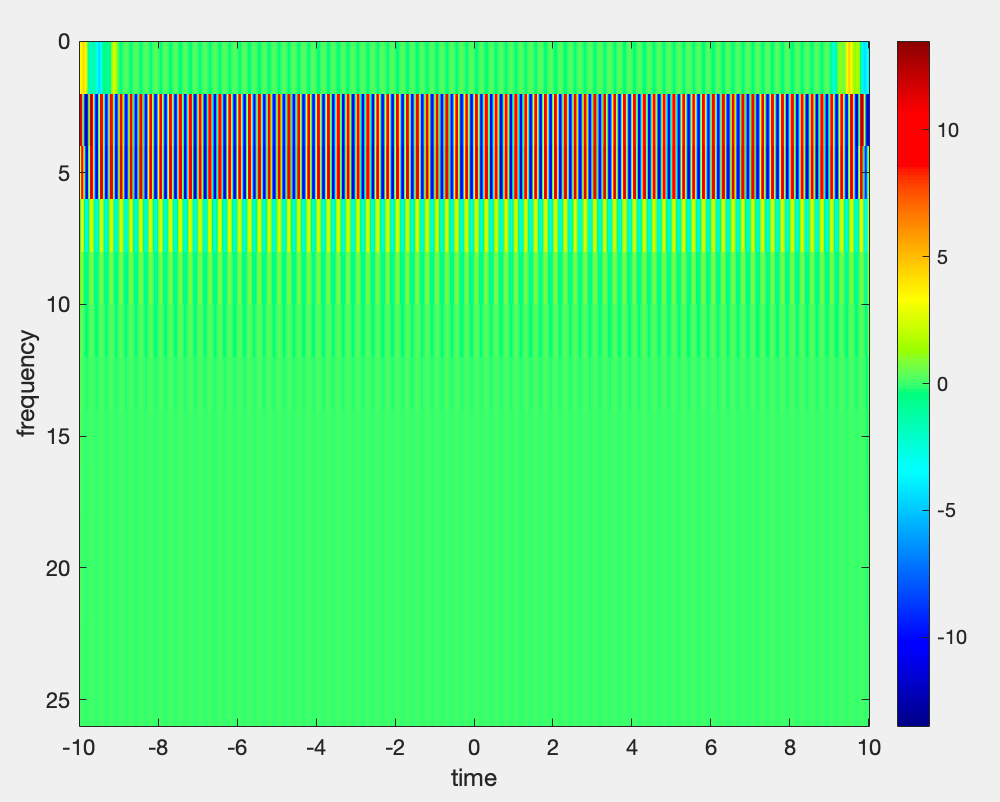
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
% wavelet parameters
fs = 100;
wTime = -1:(1/fs):0.99;
wFreq = 1:2:25;
n = 4;
wLength = length(wTime);

% creat test data
dataTime = -10:(1/fs):10;
data = sin(2*pi*4*dataTime);
data = [zeros(1,wLength/2) data zeros(1,wLength/2)];

% initialize matrix
wavelet_conv = zeros(length(wFreq),length(dataTime));

for i = 1:length(wFreq)
  f = wFreq(i);
  s = n/(2*pi*f);
  wavelet = cos(2*pi*f*wTime).*exp(-(wTime.^2)/(2*s^2));
  kernel = fliplr(wavelet);
  conv_result = conv(data,kernel,'same')/sum(kernel);
  wavelet_conv(i,:) = conv_result(wLength/2:wLength/2+length(dataTime)-1);
end

% plot
figure;
imagesc(dataTime, wFreq, wavelet_conv)
colormap("jet")
colorbar
xlabel('time')
ylabel('frequency')

注意结果存在边际效应（side effect），在4Hz的地方存在一定的方差

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np
import matplotlib.pyplot as plt

# wavelet parameters
fs = 100
wTime = np.arange(-1, 1, 1/fs)
wFreq = np.arange(1, 26, 2)
n = 4
wLength = len(wTime)

# create test data
dataTime = np.arange(-10, 10, 1/fs)
data = np.sin(2*np.pi*4*dataTime)
data = np.concatenate((np.zeros(wLength//2), data, np.zeros(wLength//2)))

# initialize matrix
wavelet_conv = np.zeros((len(wFreq), len(dataTime)))

for i in range(len(wFreq)):
    f = wFreq[i]
    s = n/(2*np.pi*f)
    wavelet = np.cos(2*np.pi*f*wTime) * np.exp(-(wTime**2)/(2*s**2))
    kernel = np.flip(wavelet)
    conv_result = np.convolve(data, kernel, 'same')/np.sum(kernel)
    wavelet_conv[i, :] = conv_result[wLength//2:wLength//2+len(dataTime)]

# plot
plt.figure()
plt.imshow(wavelet_conv, aspect='auto', extent=[min(dataTime), max(dataTime),  max(wFreq), min(wFreq) ], cmap='jet')
# 注意这里max(wFreq)和min(wFreq)需要对换
plt.colorbar()
plt.xlabel('time')
plt.ylabel('frequency')
plt.show()

Complex-valued Morlet Wavelet

数学公式：

Ae−t2/2s2ei2πftwhereA=1(sπ)1/2Ae^{-t^2/2s^2}e^{i2\pi ft} \quad \text{where} A=\frac{1}{(s\sqrt{\pi})^{1/2}}

左侧部分是Gaussian，右侧部分是complex sinnsoid。

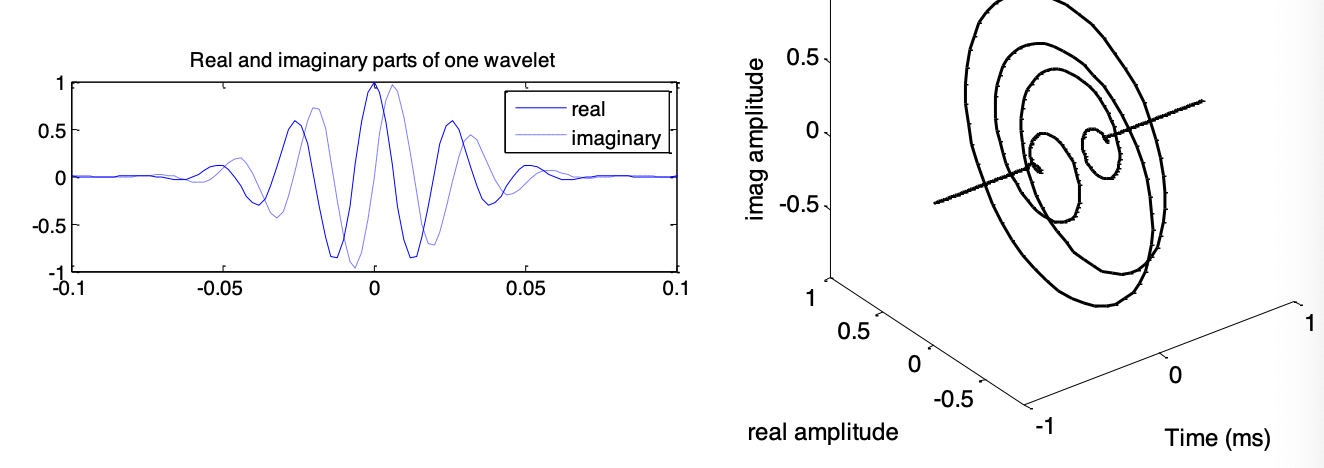
Q：complex wavelet是什么？

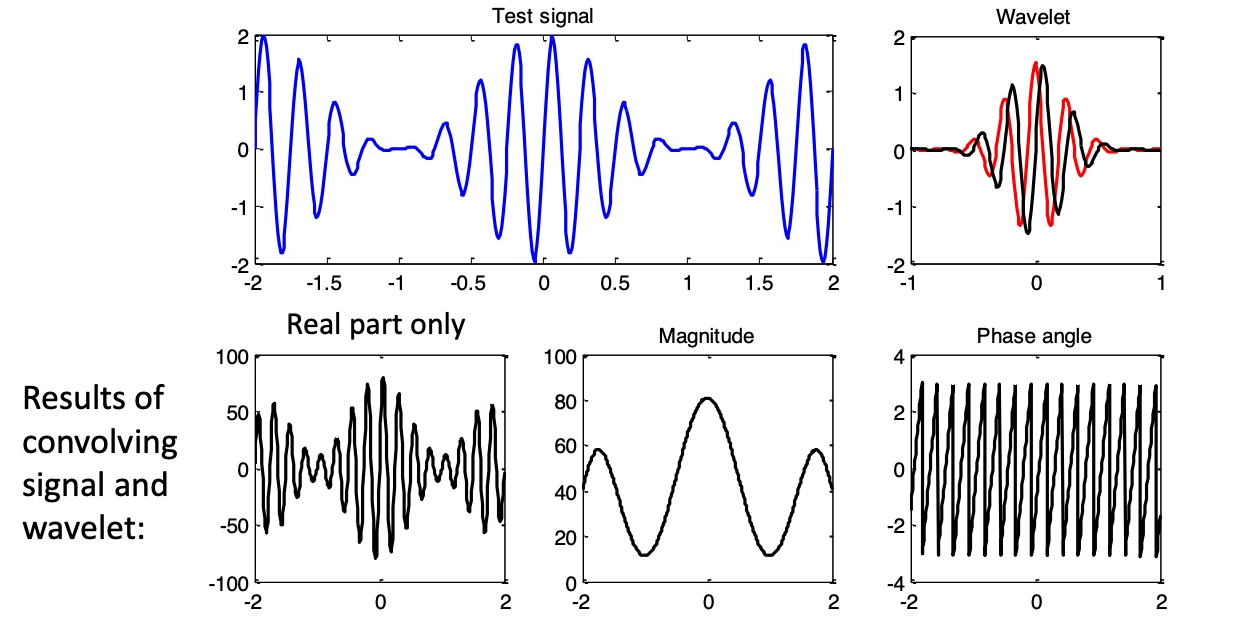
complex wavelet的实数部分，虚数部分和三维空间图如下

Q：卷积的结果怎么看？

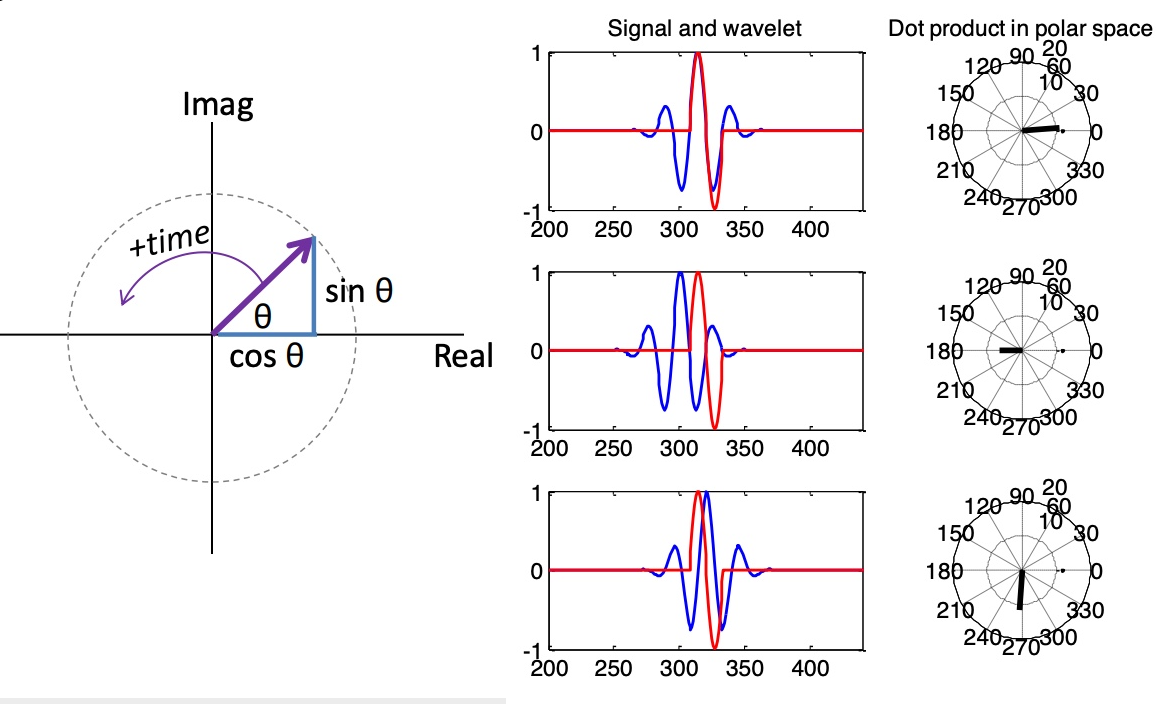
complex wavelet convolution卷积结果是在复平面的向量。

complex vector的幅值（magnitude） 表示signal在wavelet frequency上功率（power）如何随着时间变化（不受phase影响）

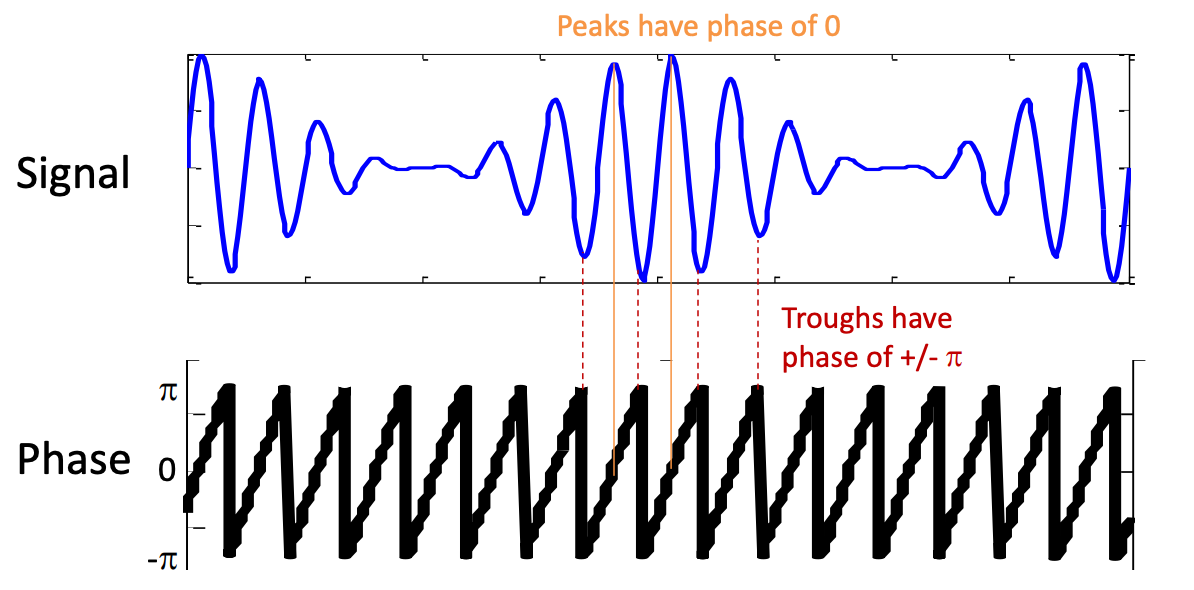
complex vector的角度（phase） 表示wavelet和signal的相位关系

complex vector的实数部分（real part）是信号经过band-pass filter之后的结果

卷积结果的real part，magnitude，和phase angle

如何分析phase的图像

Q：如何选择wavelet的参数？

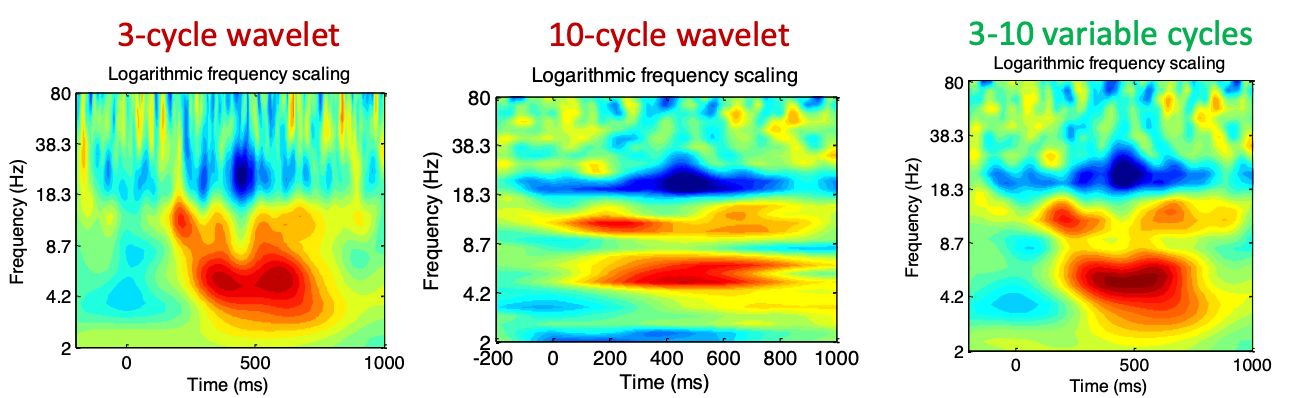
number of cycles n：n决定了wavelet的宽度。n越大，频率分辨率（frequency precision）越好，空间分辨率（temporal precision）越差。

通常情况下，如果想要研究瞬时变化（transient），我们通常会选择3-4 个cycle，想要研究频率变化，我们一般会选择7-10个cycle。当然我们也可以在不同的频率上面使用不同的cycle 数目。

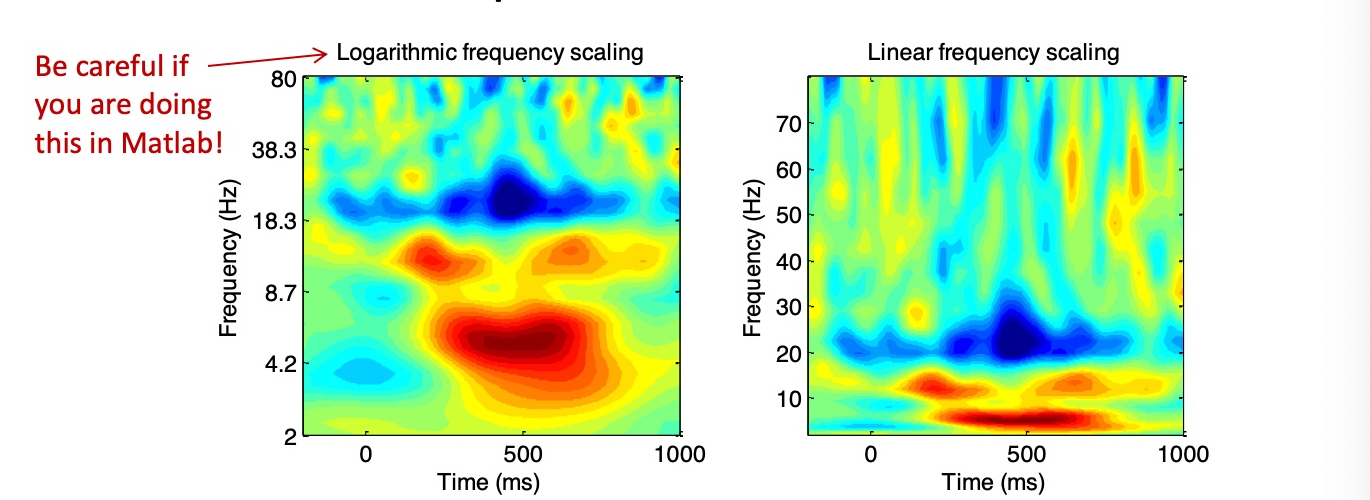
y-axis的刻度（scaling）：

指数logarithmic坐标轴可以凸显出低频区间

线性linear坐标轴可以凸显出高频区间

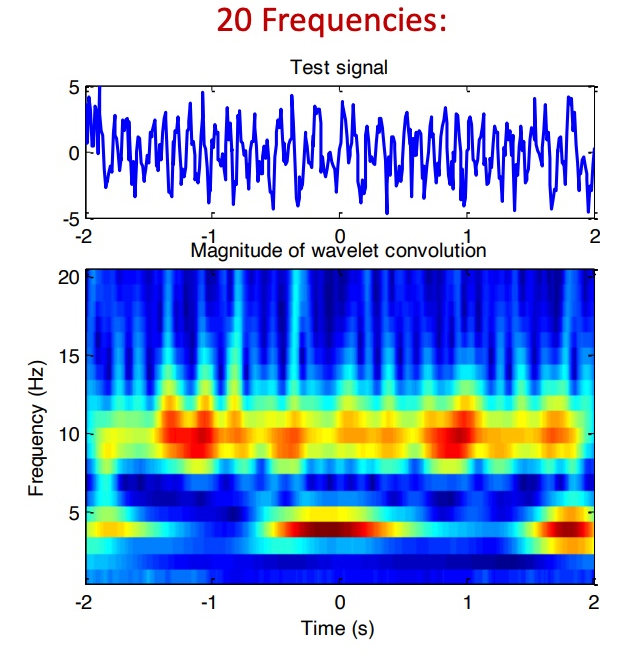
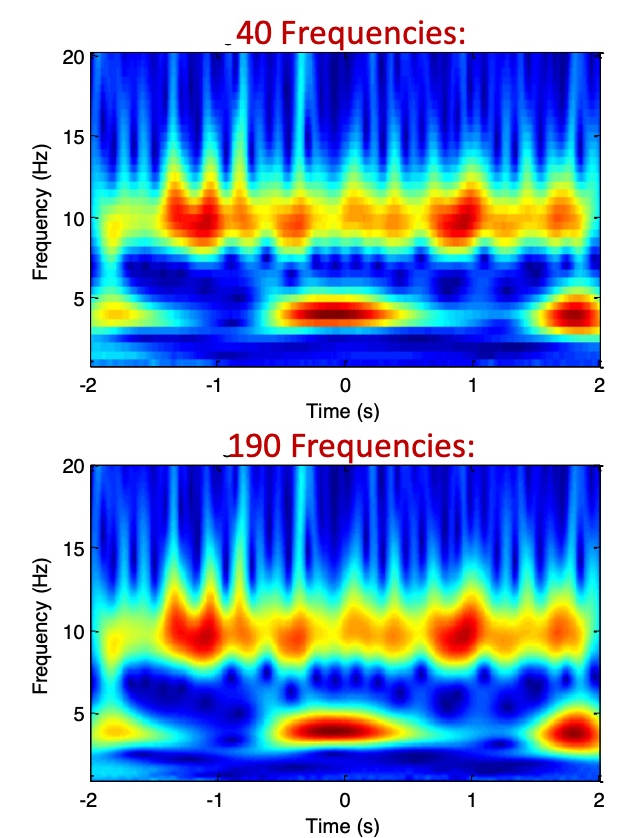
number of frequency：

频率的数量越多，则出来的结果分辨率越高，但是当频率高到一定程度之后，再增加频率数量则没啥太大意义。

length of wavelet：长度保证两端可以趋近为0，没有最大长度限制。要求wavelet的中间在t=0处，且采样频率（sampling rate）和信号的一致。

代码

！练习

假设我有一个60s长的采样频率为100Hz的信号，我想要进行complex-based wavelet convolution，则代码应该如何编写？

Maltab

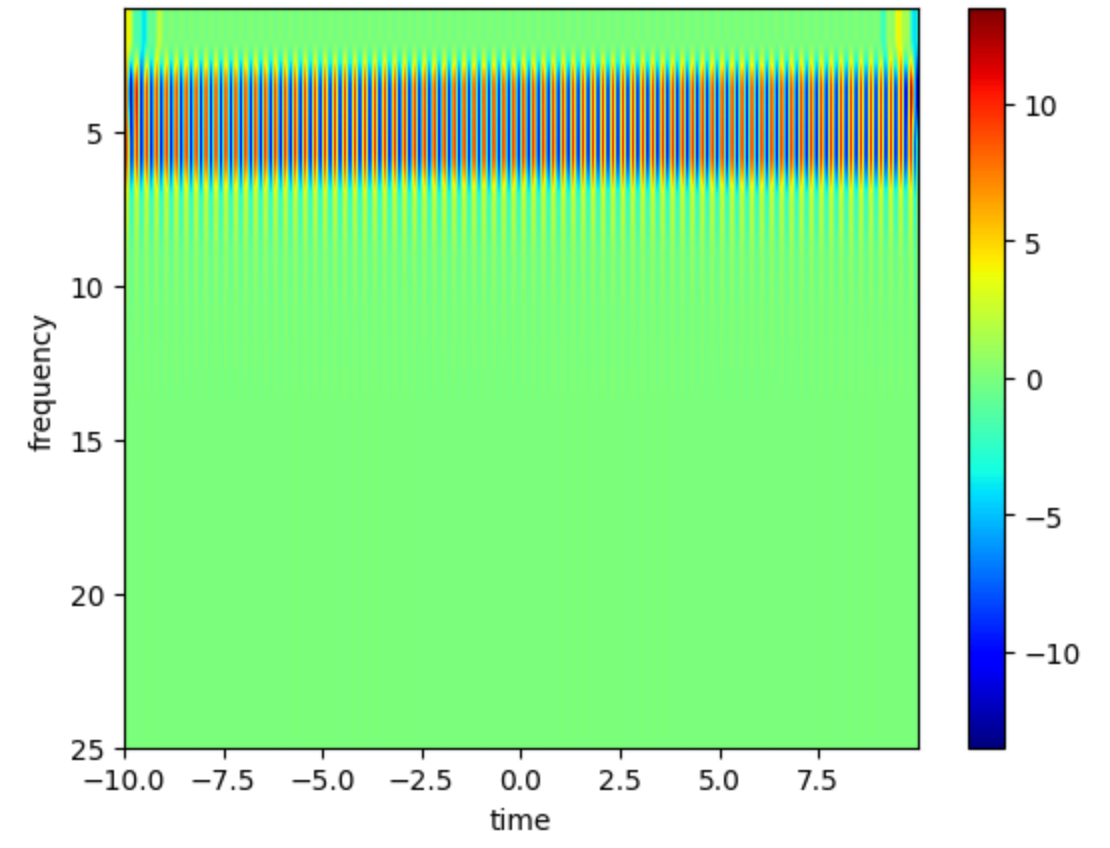
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
% wavelet parameters
fs = 100;
wTime = -1:(1/fs):0.99;
wFreq = 1:2:25;
n = 4;
wLength = length(wTime);

% creat test data
dataTime = -10:(1/fs):10;
data = sin(2*pi*4*dataTime);
data = [zeros(1,wLength/2) data zeros(1,wLength/2)];

% initialize matrix
wavelet_conv = zeros(length(wFreq),length(dataTime));

for i = 1:length(wFreq)
  f = wFreq(i);
  s = n/(2*pi*f);
  A = 1/((s*sqrt(pi))^0.5);
  wavelet = A.*exp(-(wTime.^2)/(2*s^2)).*exp(1i*2*pi*f.*wTime);
%   wavelet = exp(2*1i*pi*frex(fi).*time) .* exp(-time.^2./(2*(numcycles(fi)/(2*pi*frex(fi)))^2));
  kernel = fliplr(wavelet);
  conv_result = conv(data,kernel,'same');
  wavelet_conv(i,:) = conv_result(wLength/2:wLength/2+length(dataTime)-1);

end

% plot
figure;
imagesc(dataTime, wFreq, abs(wavelet_conv))
colormap("jet")
colorbar
xlabel('time')
ylabel('frequency')

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
import matplotlib.pyplot as plt

# wavelet parameters
fs = 100
wTime = np.arange(-1, 1.01, 1/fs)
wFreq = np.arange(1, 26, 2)
n = 4
wLength = len(wTime)

# create test data
dataTime = np.arange(-10, 10.01, 1/fs)
data = np.sin(2*np.pi*4*dataTime)
data = np.concatenate((np.zeros(wLength//2), data, np.zeros(wLength//2)))

# initialize matrix
wavelet_conv = np.zeros((len(wFreq), len(dataTime)))

for i in range(len(wFreq)):
    f = wFreq[i]
    s = n/(2*np.pi*f)
    A = 1/np.sqrt(s*np.sqrt(np.pi))
    wavelet = A * np.exp(-(wTime**2)/(2*s**2)) * np.exp(1j*2*np.pi*f*wTime)
    kernel = np.flip(wavelet)
    conv_result = np.convolve(data, kernel, 'same')
    wavelet_conv[i, :] = conv_result[wLength//2:wLength//2+len(dataTime)]

# plot
plt.figure()
plt.imshow(np.abs(wavelet_conv), aspect='auto', extent=[min(dataTime), max(dataTime), max(wFreq), min(wFreq)], cmap='jet')
plt.colorbar()
plt.xlabel('time')
plt.ylabel('frequency')
plt.show()

后续分析

使用real(wavelet_conv) = 投射到实数轴的结果 = 经过带通滤波器

使用abs(wavelet_conv) = 向量的幅值（magnitude）= 数据在wavelet frequency上面的power大小

使用angle(wavelet_conv) = 向量的角度（angle）= 数据的相对于某个时间点的wavelet的phase angle

可以使用FFT → 相乘 → IFFT替代卷积conv来提高运算效率

声明：此blog内容为上课笔记，仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权，请联系aursus.blog@gmail.com删除。