生物医学工程 | EEG分析 - 希尔伯特变换
希尔伯特变换|Hilbert transform
大致操作方法:先进行bandpass filter,然后进行Hilbert transform获得complex signal,从而分离出amplitude和phase
目的:通过添加虚数部分,从实数信号中获得瞬时幅度amplitude和相位phase
📌我们并不改变实数部分,只是在这基础上添加了虚数部分
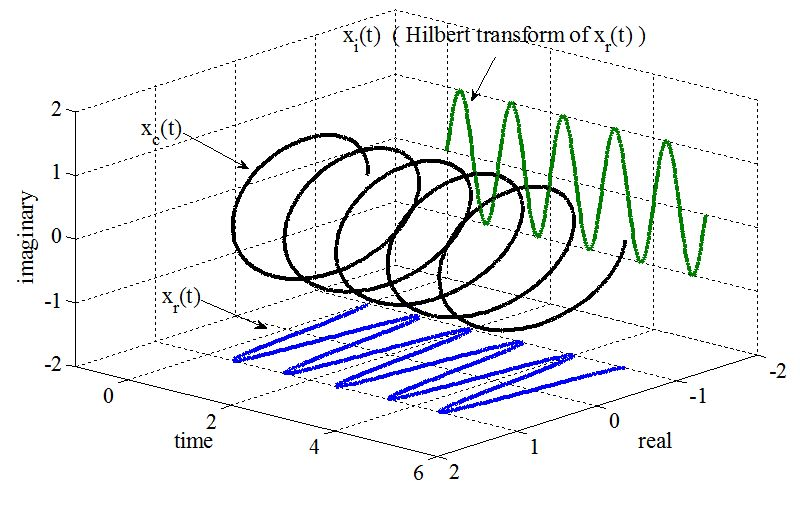
数学定义
假设我们已知信号叫做,则Hilbert transform为:
imag信号是real信号shift 之后的结果 。比如原始信号为,则Hilbert变换之后的结果为
代码
MATLAB代码
1 | % 自己写hilbert的内部代码 |
1 | % 使用Hilbert函数 |
Python代码
1 | # 自己写hilbert的内部代码 |
1 | # 使用Hilbert函数 |
滤波|Filter
在使用Hilbert之前需要对数据进行滤波处理,不然过大的带宽会导致结果难以解释。
常见的两种滤波器:有限脉冲响应Finite impulse response (FIR);无限脉冲响应Infinite impulse response (IIR)
FIR比起IIR的优点和特点:
- FIR的kernel函数在正无穷和负无穷的地方都等于0
- wavelet就算一种FIR滤波器
- 比起IIR,更推荐使用FIR,因为其既稳定又不容易引入非线性相位失真( nonlinear phase distortions)
- 但是FIR的计算花费更高
设计滤波器需要注意的事情:
- 滤波器频谱图上尖锐的边缘(sharp edge)会导致时域的ripples,因此我们最好设计平台状(Plateau-shaped)的滤波器,并尽可能保障过渡地带(transition zones)是(最大频率-最小频率)的10%~25%
代码
MATLAB代码
最常见的函数firls和firl,还有一些其他的函数
firls:最小二乘法线性相位FIR滤波器(Least-squares linear-phase FIR filter)
1 | b = firls(n, f, a) |
n:n表示filter order。且对应的kernel的长度是n+1(指的是point number而不是时间)。n没有上限,越高越好,但是会增加计算量;n的下限是最低频率的2-5倍(比如最低频率为10Hz,则通常使用200-500ms时间长度对应的kernel)
f:f表示滤波器各点的x坐标,是滤波器各点频率在经过scale之后的相对值(通过scale令Nyquist 频率=1)。比如f = [0, 0.1, 0.15, 0.3, 0.35, 1];
a:a表示滤波器各点的y坐标,并且scale到[0,1]。比如a = [0 0 1 1 0 0];注意a和f的长度一致
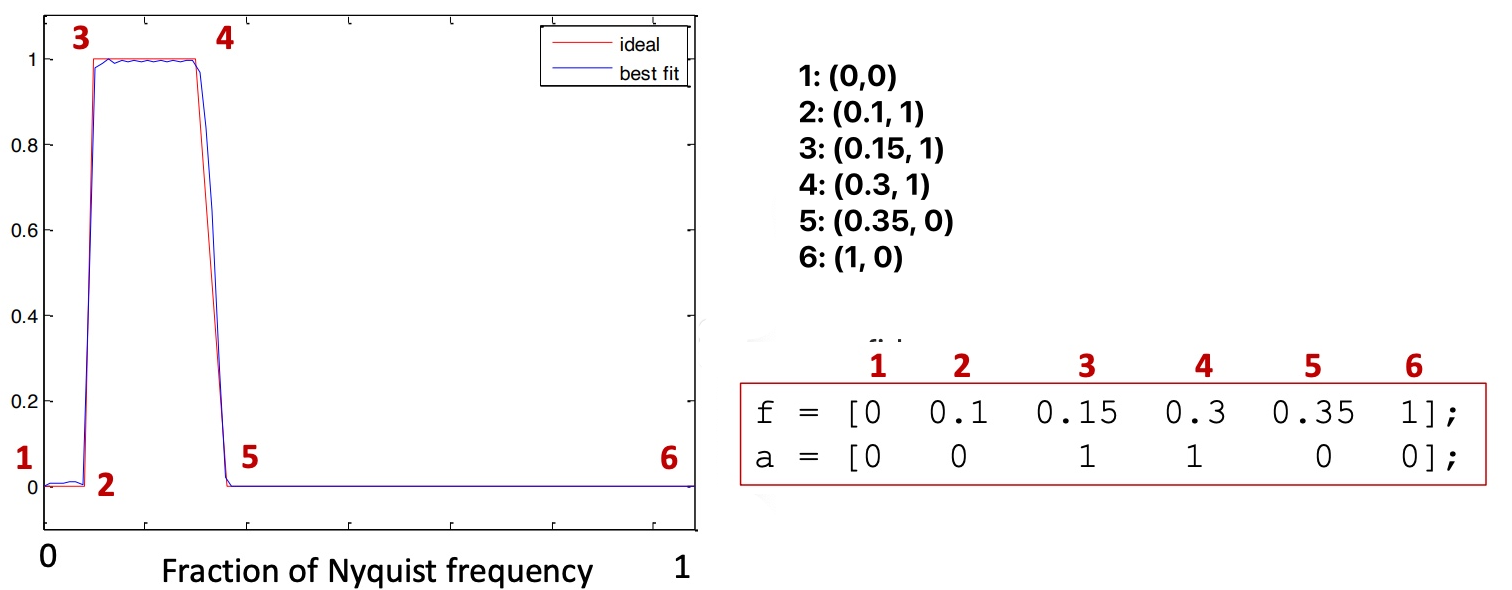
fir1:基于窗口的FIR滤波器(Window-based FIR filter)
声明:此blog内容为上课笔记,仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权,请联系aursus.blog@gmail.com删除。