生物医学工程 | 机器学习 - 主成分分析法 PCA

概念

目的：降维

input $x \subset R^d$ ， $\{x^{(i)}; i = 1, ..., n\}$

output $Z \subset R^k$

$F: X \rightarrow Z$ , $k<<d$

i 表示有几个sample（共n个），j表示有几个feature（共d个）

目的：将所有的feature normalize为mean= $\mathbb{E}[x_j^{(i)}]$ =0，variance= $Var[x_j^{(i)}]$ =1的数据

方法：

x_j^{(i)}\leftarrow \frac{x_j^{(i)}-\mu_j}{\sigma_j}\\ \text{where, }\mu_j=\frac{1}{n}\sum_{i=1}^n x_j^{(i)},\ \sigma^2_j=\frac{1}{n}\sum_{i=1}^n(x_{j}^{(i)}-\mu_j)^2

如果我们能够确定不同的feature都有相同的scale，则可以表示

？parameter estimation使用的是EM算法

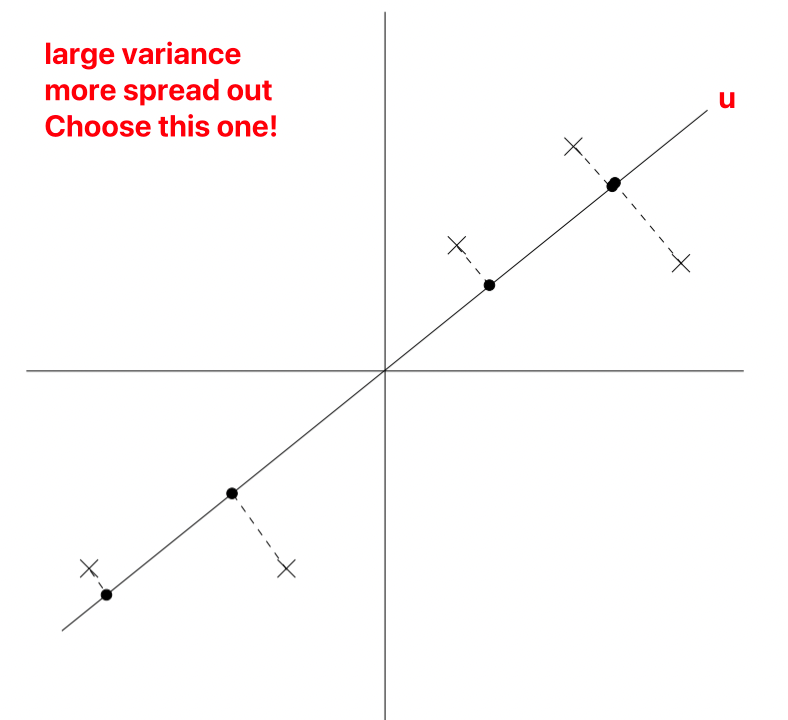
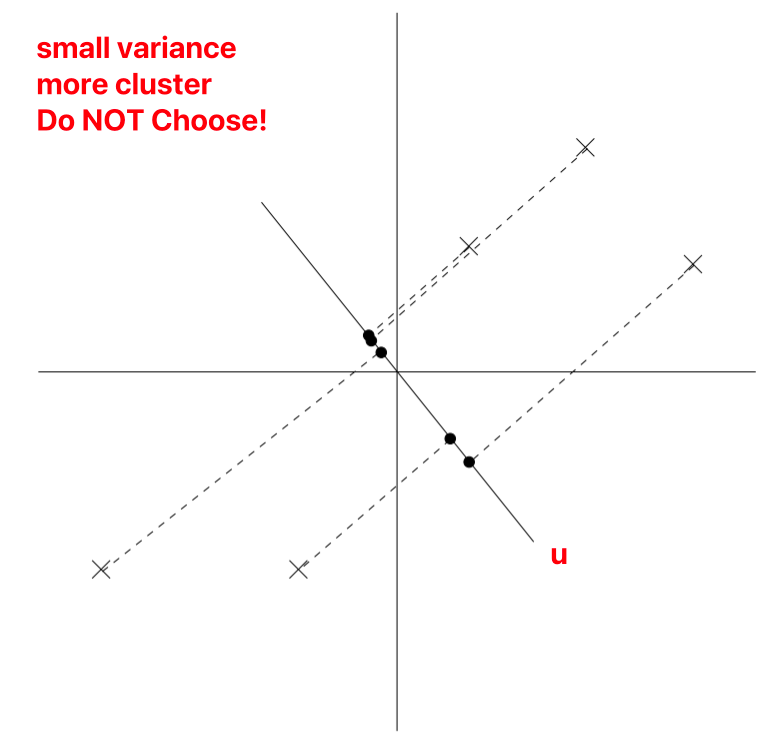
u为unit vector，x为sample，在图上标示为不同的点

在projection（将2d降维1d的时候），为了保留更多的信息，我们选择projection data 的variance较大的，也就是投影点分布更加均匀的。

因为经过normalize了，所以u一定经过原点。

点x在向量u上面点投影是 $x^Tu$ ，

Projection的求法：

||Proj_u(x)||_2=|x^Tu|

Variance的求法：

Var(Proj_u(x))=|x^Tu|^2

所有点x在单个u上面投影的variance：

\frac{1}{n}\sum_{i=1}^n(x^{(i)^T}u)^2=\frac{1}{n}\sum_{i=1}^nu^Tx^{(i)}x^{(i)^T}u\\=u^T(\frac{1}{n}\sum_{i=1}^nx^{(i)}x^{(i)^T})u =u^T\hat\Sigma u

如果 $||u||_2=1$ ，则principal eigenvector可以化简为 $\hat\Sigma = \frac{1}{n}\sum_{i=1}^nx^{(i)}x^{(i)^T}$ ，即

\max_{||u||_2=1}u^T\hat\Sigma u =\lambda_1

其中 $\lambda\_1$ 表示first eigenvalue of $\hat\Sigma$ principle eigenvalues，此时的u取的是1st principal eigenvector of $\hat\Sigma$

x最好的1D方向是 1st eigenvectors of covariance，即 $v_1\bar\Sigma$ 。可以使用pytorch的torch.lobpcg函数

如果我们想把数据投射到1D中，则选择 $u$ to be principal eigenvector of $\Sigma$ 。

降维投射完毕的数据： $X.mm(V)$ ，其中V为前k个eigenvector，size (d, k)。 $X$ 从 $m \times d$ 维度降为 $m \times k$

如果我们想把数据投射到 $k$ D中，

方法一：选择 $ u_1, u_2, …, u_k$ to be the top $k$ eigenvectors of $\Sigma$ 。

\max_{u_1,u_2,...,u_k}\sum_{i=1}^u\left|\left|\left[\begin{matrix}u_1^Tx^{(i)}\\u_2^Tx^{(i)}\\...\\u_k^Tx^{(i)} \end{matrix}\right] \right|\right|_2^2=v_1,v_2,...,v_k

方法二：

\min_{u_1,u_2,...,u_k}\sum_{i=1}^n||x_i-\bar x_i||_2^2\\ =\sum_{i=1}^n||x_i-\sum_{l=1}^k(u^T_lx_i)u_l||_2^2

其中 $\bar x_i$ 表示reconstruction example given by basic component

声明：此blog内容为上课笔记，仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权，请联系aursus.blog@gmail.com删除。