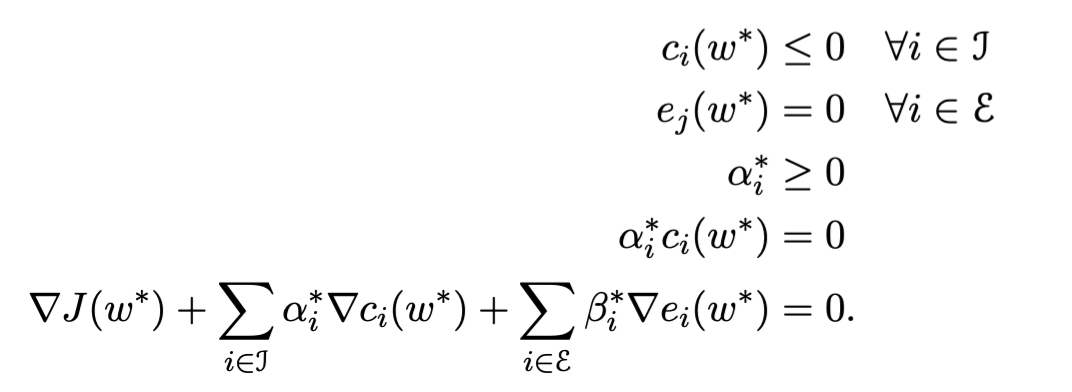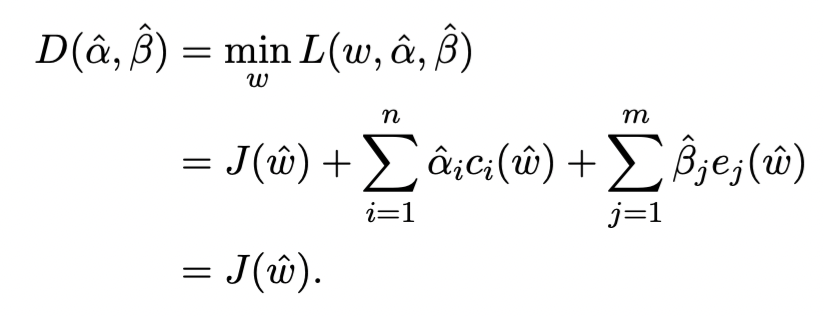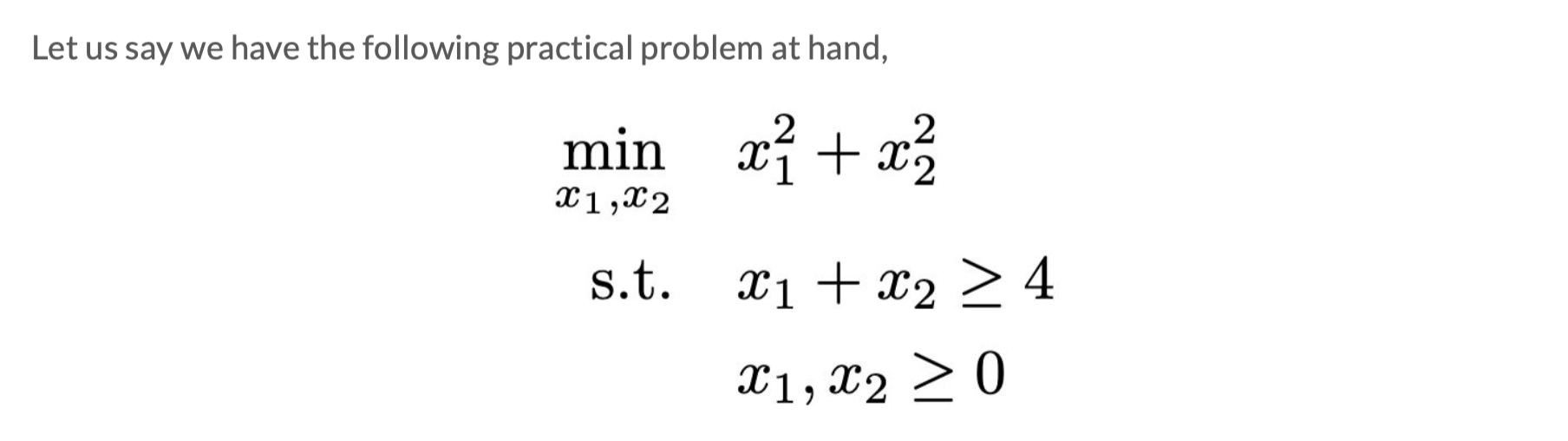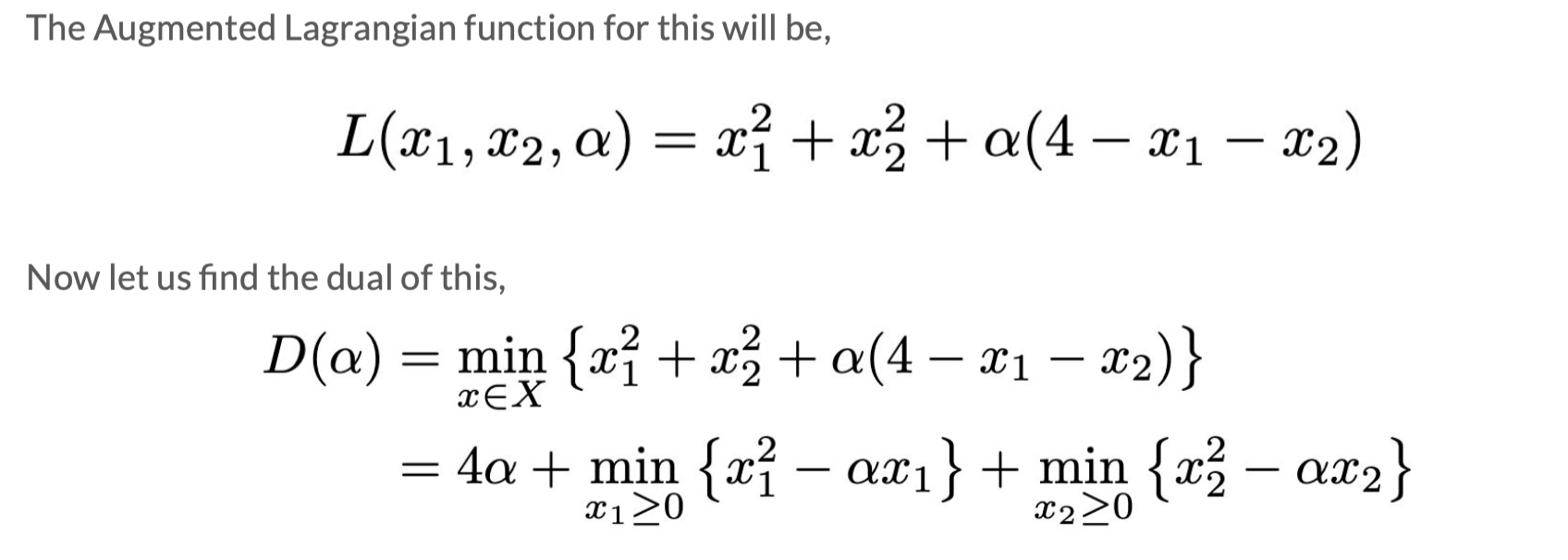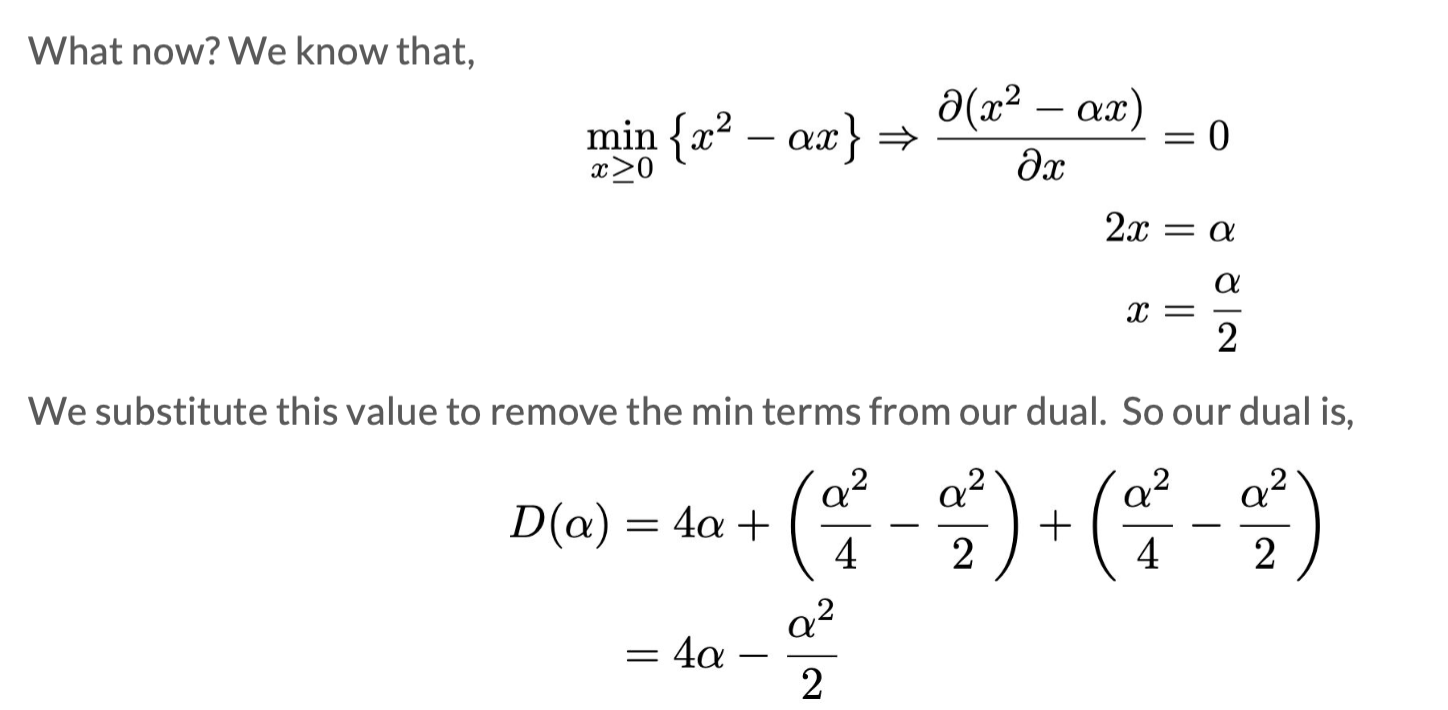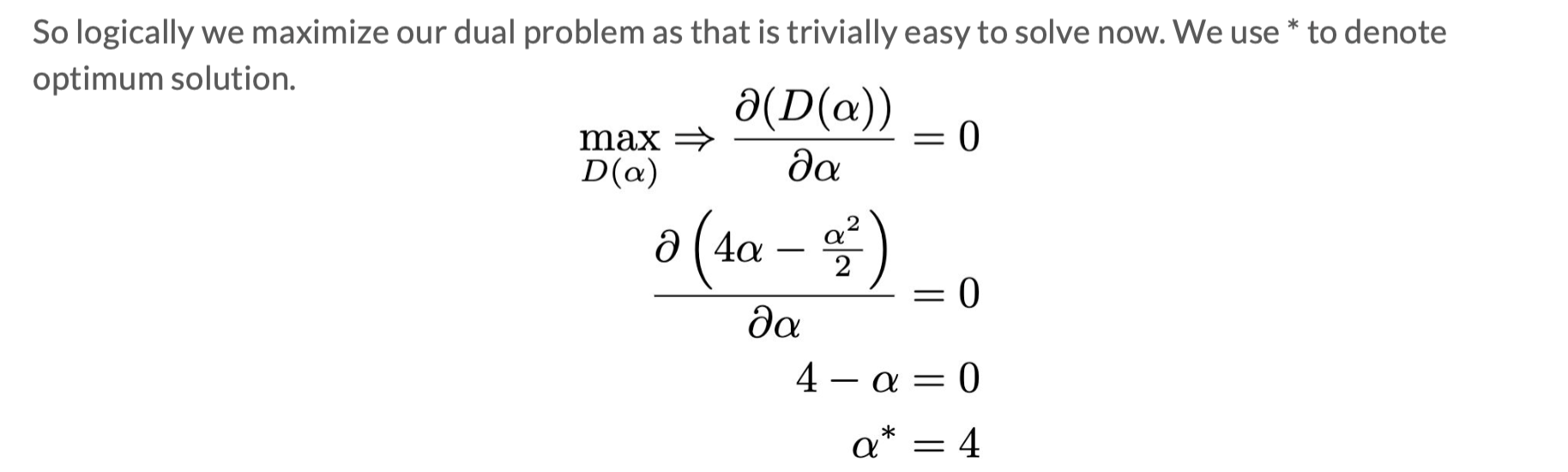目的:一般算法如MLE只能够求无约束的式子的最优化值,如 maxωm1∑l(ω;xi,ji)。但是如果我们遇到了有constraint的算法,则需要用Duality,LP,QP来解决这类问题。此外,Duality,LP,QP也可以解决第一类没有constraint的类型
Duality Problem
题目类型
ωminJ(ω)s.t. ci(ω)≤0, for i∈jei(ω)=0, for i∈ϵ——(0)
Augmented Lagrange
L(ω,α,β)=J(ω)+i∈j∑αici(ω)+i∈ϵ∑βiei(ω)——(1)
dual feasbile指 αi≥0,βi∈R
定理1
从式(1)可以求出来
α≥0,βmaxL(ω,α,β)={J(ω), if ω is feasible∞,otherwise——(2)
尤其是,如果J∗=minωJ(ω),且ci(ω)≤0且ei(ω)=0,则
J∗=ωminα≥0,βmaxL(ω,α,β)
证明见pdf
定理2|weak duality
定义Lagrange dual function如下
D(α,β)=ωminL(ω,α,β)
则上式满足
D(α,β)≤J(ω)
for all feasible $ \omega $and α≥0 and β。尤其是
D∗:=α≥0,βmaxωminL(ω,α,β)≤ωminα≥0,βmaxL(ω,α,β)=J∗
注意:weak duality不一定要求J(ω)是convex的
定理3|strong duality
如果J(ω),ci,ei都是convex,且下列constraint qualification满足:
存在一个$ \omega 使得c_i(\omega)<0$, for all i∈j
则式(1)满足
D∗:=α≥0,βmaxωminL(ω,α,β)=ωminα≥0,βmaxL(ω,α,β)=J∗
注意D∗=maxα>0,βD(α,β)是duality problem optimal 的情况,J∗=minωJ(ω)是original problem optimal的情况。
KKT condition
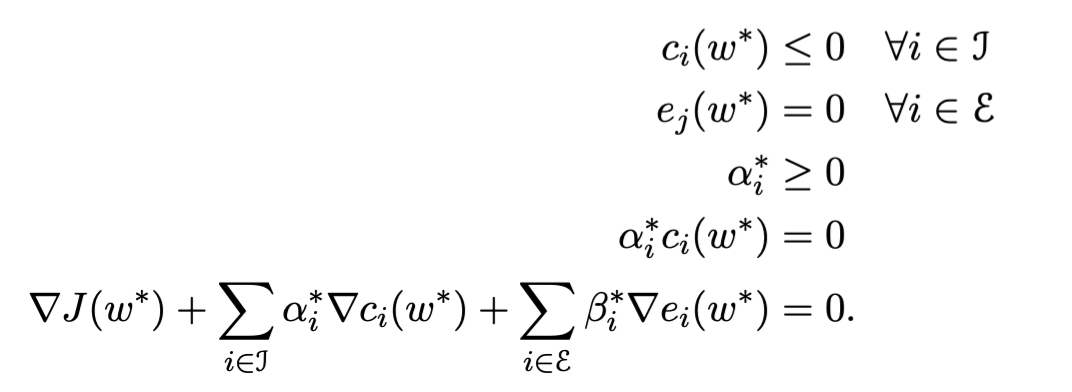
如果primal problem is convex,则KKT条件充分且必要。即如果ω^和(α^,β^)满足KKT条件,则ω^和(α^,β^)是primal和dual optimal,即
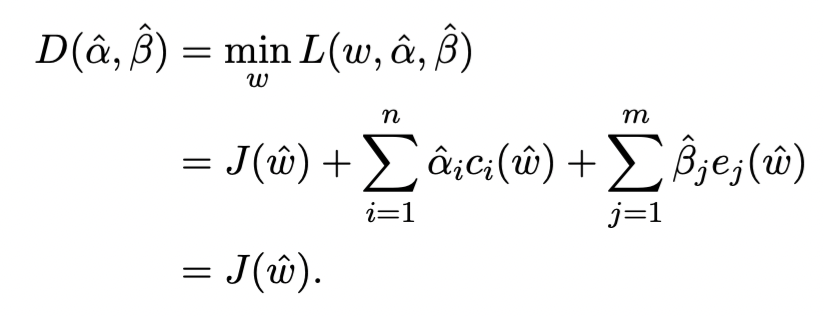
Linear Problem
题目满足
min cTw⇒J(ω)s.t. Aω=b⇒ej(ω)ω≥0⇒ci(ω)
$ D(\alpha, \beta) $for LP is still a LP
Quadratic Problem
题目满足
minωTGω+ωTds.t. Aω=bω≥0
具体怎么带入duality的可以参考pdf
小结

例题
一般思路:
1)写出L;
2)D=min(L):对w求偏导(有时候有两个),用 α 和 β 表示 w,得到 D;
3)maxD 得 D∗,α∗,β∗:对D求偏导或者用KKT条件得到 D∗,从而得到 α∗,β∗
4)J∗,w∗:带入第二步的式子,得到w*。J*=D*


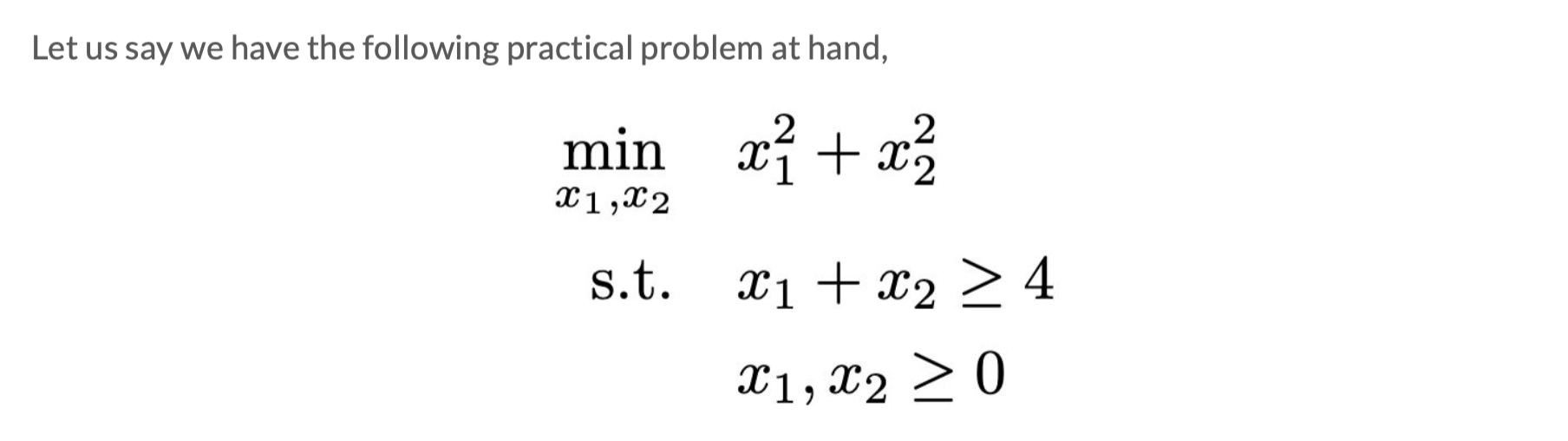
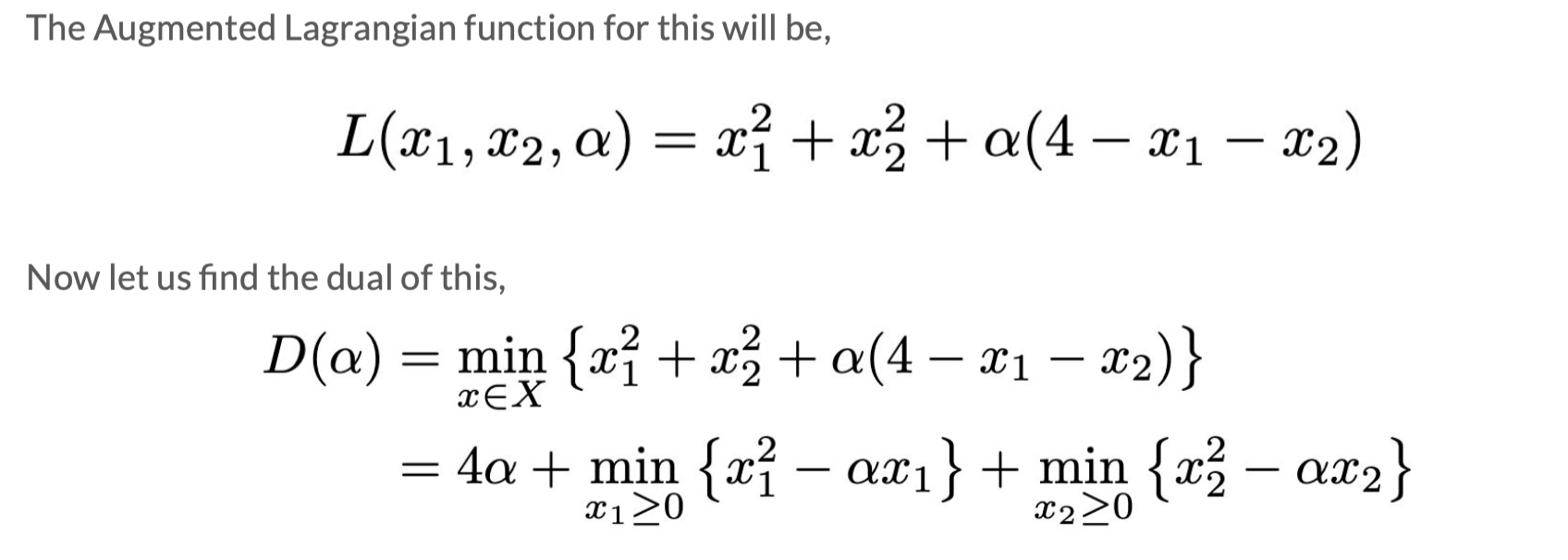
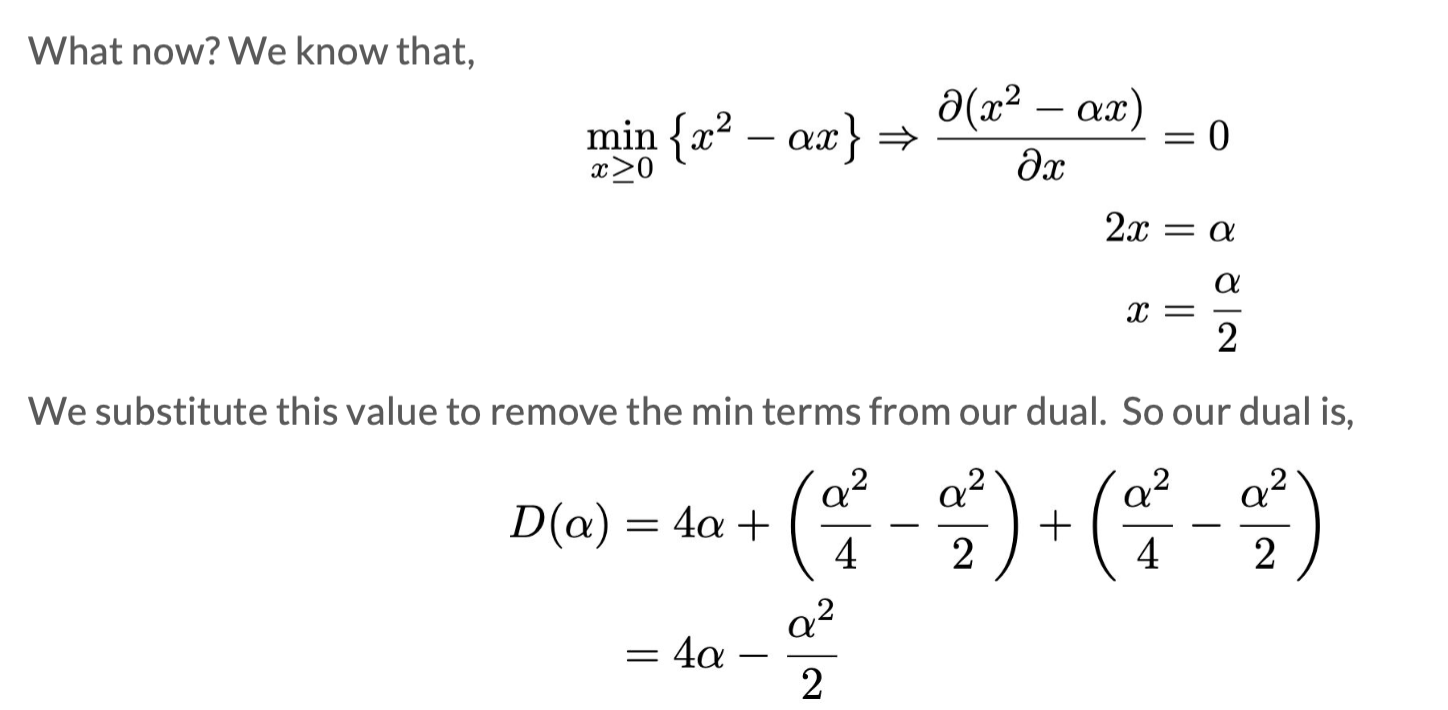
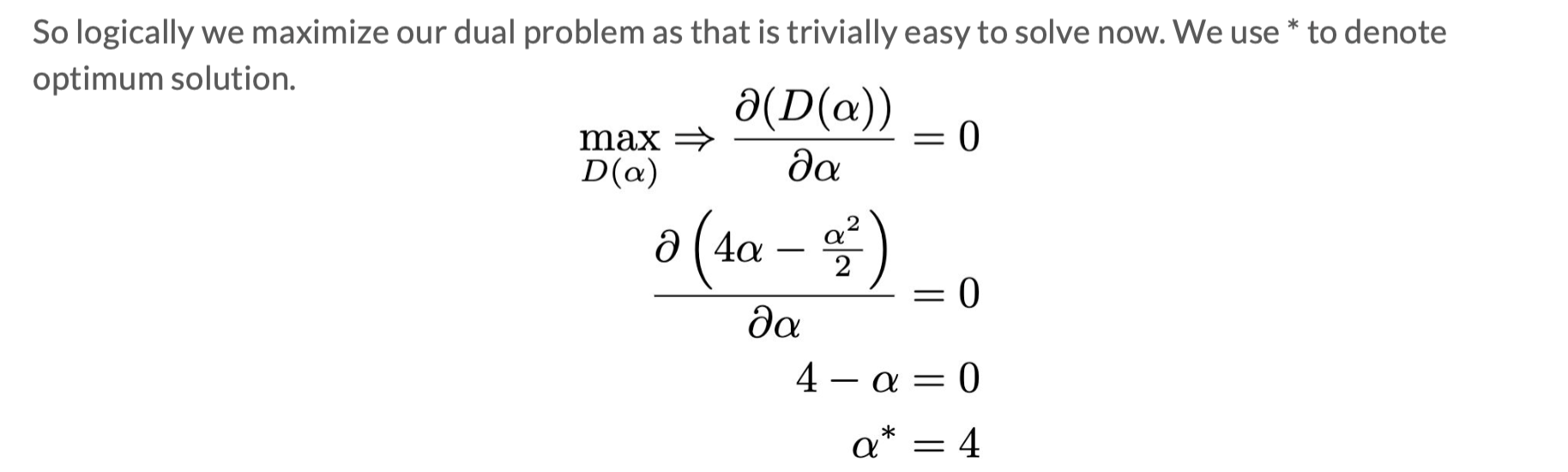
声明:此blog内容为上课笔记,仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权,请联系aursus.blog@gmail.com删除。