K means Clustering

Assumptions

There are kk subsets C1,C2,C3,...,CkC_1, C_2, C_3, ..., C_k, and 1,...,n1, ..., n data points, and all data points satisfy the following conditions:

  1. Each point belongs to a cluster.
  2. Each cluster is non-overlapping.

Defining Distance

Z(C1,⋯ ,Ck)=∑l=1k12∣Cl∣∑i,j∈Cl∥xi−xj∥22Z ( C _ { 1 } , \cdots , C _ { k } ) = \sum _ {l = 1 } ^ { k } \frac { 1 } { 2 | C _ { l } | } \sum _ {i , j \in C _ { l }} { \| x _ { i } - x _ j\|_2 ^ { 2 }}

where ∣Ck∣|C_k| denotes the number of observations in the kth cluster.

The goal is to minimize the pairwise squared distance for each cluster.

Z(C1,⋯ ,Ck)=∑l=1k∑i∈Clk∣∣xi−μl∣∣22Z ( C _ { 1 } , \cdots , C _ { k } ) = \sum _ { l = 1 } ^ { k } \sum _ { i \in C_l } ^ { k } | | x _ { i } - \mu_l | | _ { 2 } ^ { 2 }

where

μl=1∣Cl∣∑i∈Clxi\mu _ { l } = \frac { 1 } { | C _ { l } | } \sum _ { i \in C _ { l } } x _ { i }

Iterative Objective

min⁡c1,⋯ ,ckZ(C1,⋯ ,Ck)\operatorname { m i n } _ { c _ { 1 }, \cdots , c _ { k } } Z ( C _ { 1 } , \cdots , C _ { k } )

Algorithm | Lloyd’s algorithm

Not necessarily optimal because if the initialized points are not good, it can converge to a suboptimal clustering.

  • input: x1,x2,...,xkx_1, x_2, ..., x_k
  • initial: C1,C2,...,CkC_1, C_2, ..., C_k
  • loss function

Z(C1,⋯ ,Ck)=∑l=1k12∣Cl∣∑i,j∈Cl∥xi−xj∥22Z ( C _ { 1 } , \cdots , C _ { k } ) = \sum _ {l = 1 } ^ { k } \frac { 1 } { 2 | C _ { l } | } \sum _ {i , j \in C _ { l }} { \| x _ { i } - x _ j\|_2 ^ { 2 }}

  • If not yet converged,

    1. Update centroids.
    2. Update clusters.

Choosing k: Determining Size

If Zk+1<<ZkZ_{k+1}<<Z_k, it is necessary to increase k, i.e., k→k+1k\rightarrow k+1.

Finding the position of the knee in the loss function-k function

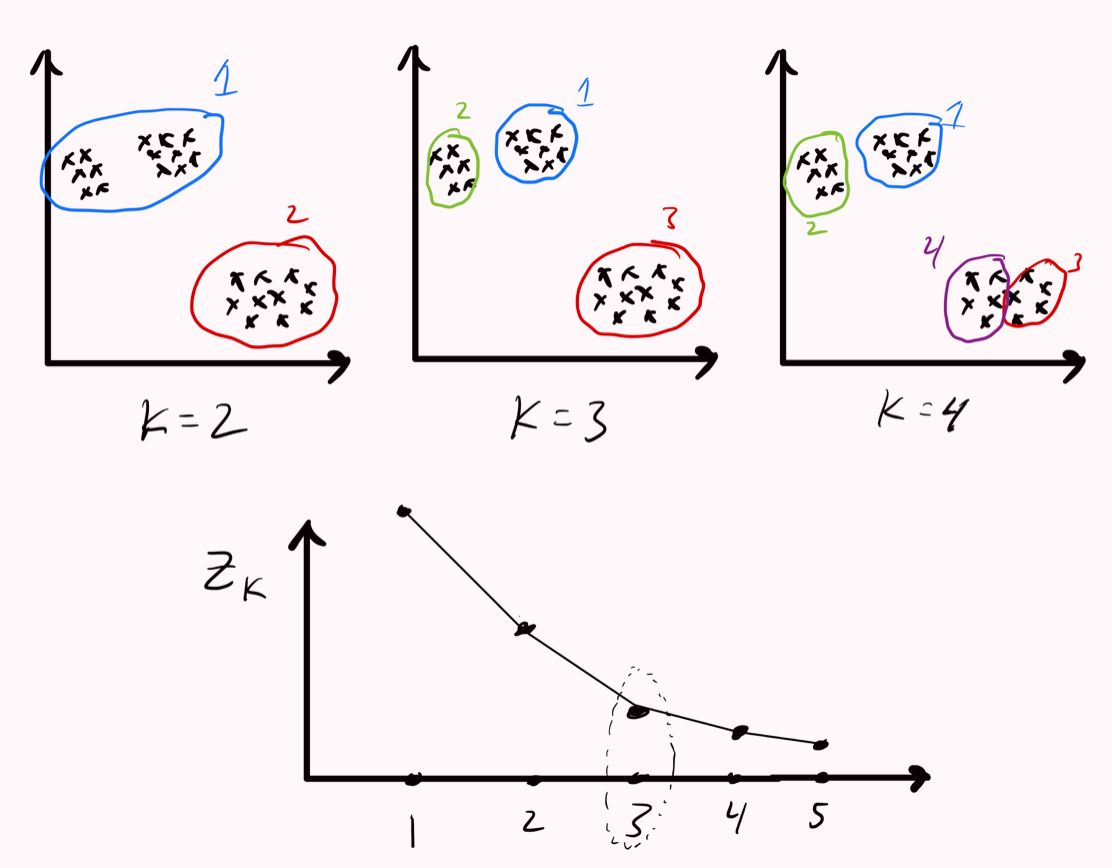
Choosing initial cluster assignment

  • Everyone tries several random initial cluster assignments and then selects the one with the lowest result using Lloyd’s algorithm.
  • Or, through the k-means++ method: randomly select the first data point as a centroid, then choose subsequent centroids based on a distance-weighted distribution from the already selected centroids.

Decision Boundaries

The region {x∈Rd  ∣  ∣∣x−μl∣∣2=∣∣x−μl′∣∣2}\{x\in \mathbb{R}^d\ \ |\ \ ||x-\mu_l||_2 = ||x-\mu_{l'}||_2\} can be computed using two cluster centroids μl\mu_l, μl′\mu_{l'}.

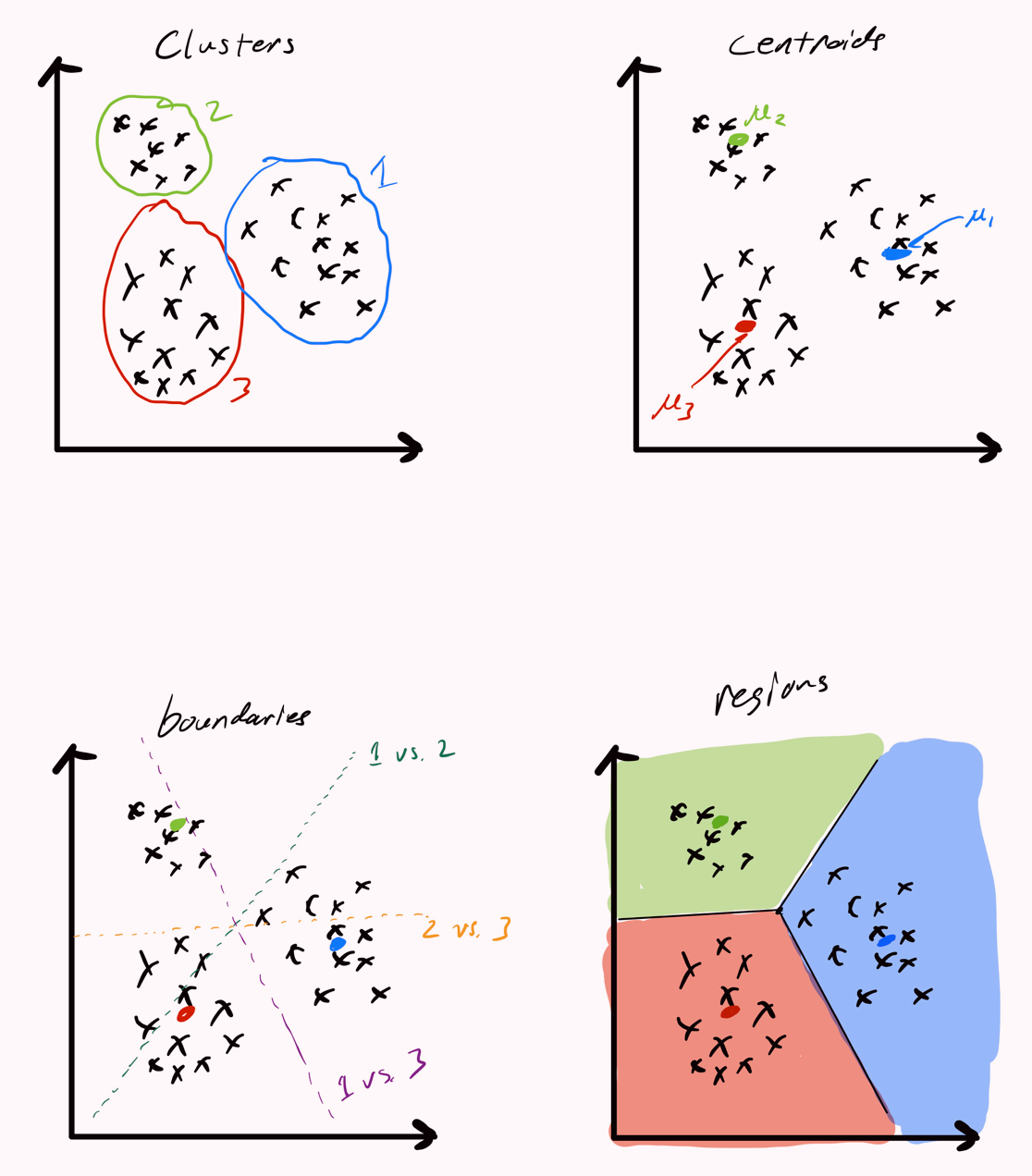
Reference:

https://www.cs.cornell.edu/courses/cs4780/2022sp/notes/LectureNotes04.html

Note: The content in this blog is class notes shared for educational purposes only. Some images and content are sourced from textbooks, teacher materials, and the internet. If there is any infringement, please contact aursus.blog@gmail.com for removal.