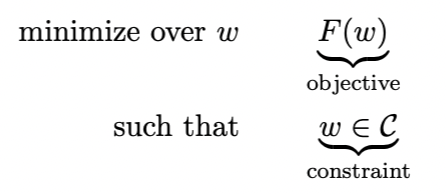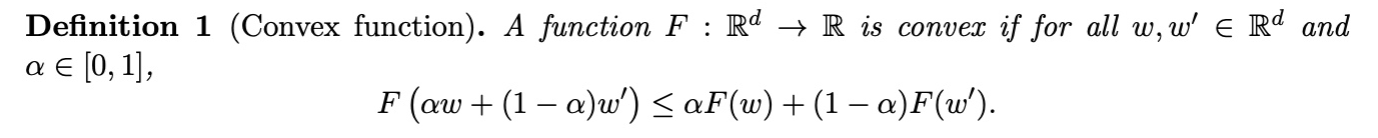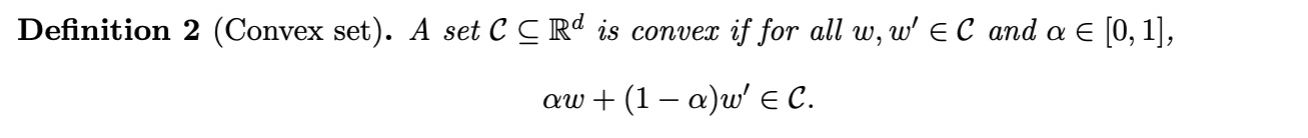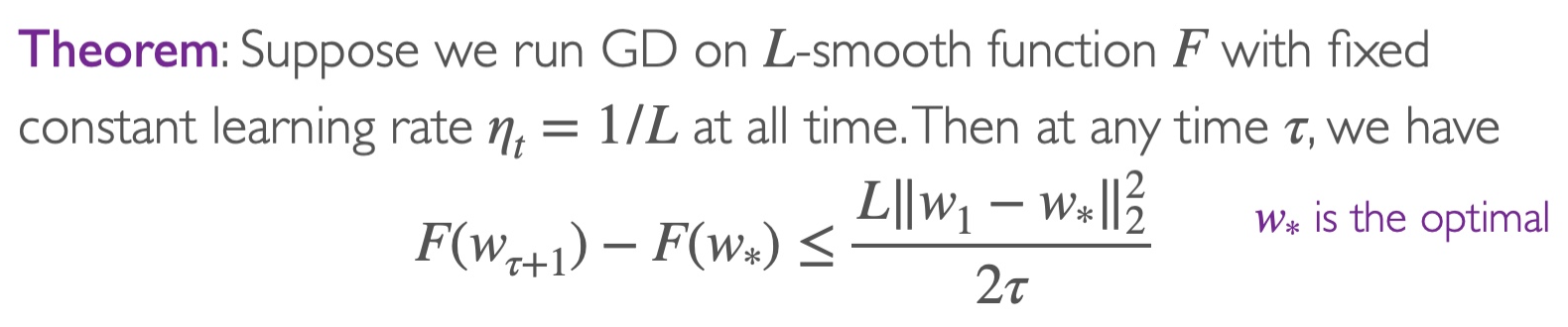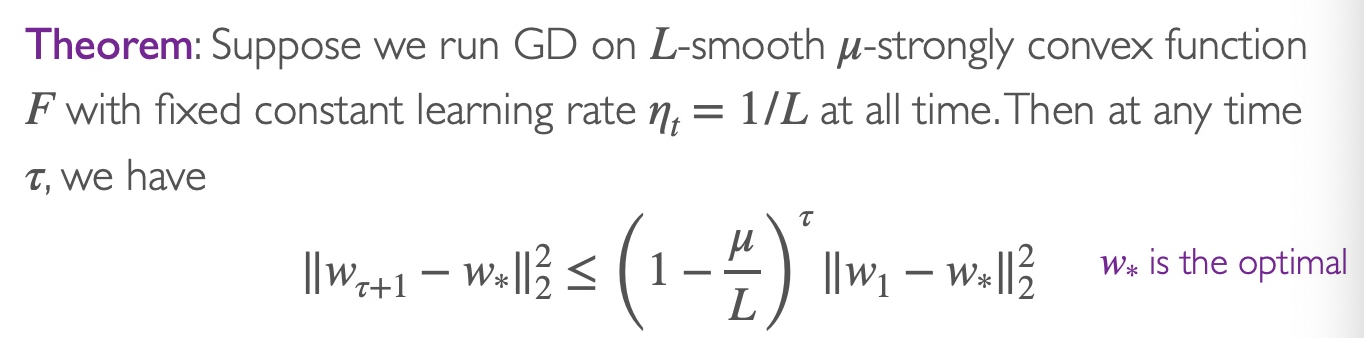Purpose: To learn effective methods for optimizing objectives - gradient descent. This method is based on a convex function.

Convex Optimization

The objective of this section is to solve the optimization problem below:

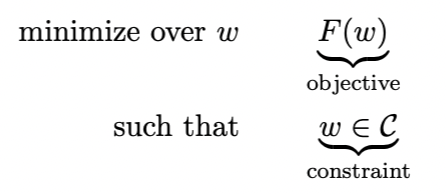
Convex Optimization Problem

Where C⊂Rd\mathscr{C}\subset \mathbb{R}^d, F:Rd→RF:\mathbb{R}^d \rightarrow \mathbb{R}. C is a convex set, and F is a convex function.

Definitions of Convex Function and Convex Set

Definition of Convex Function:

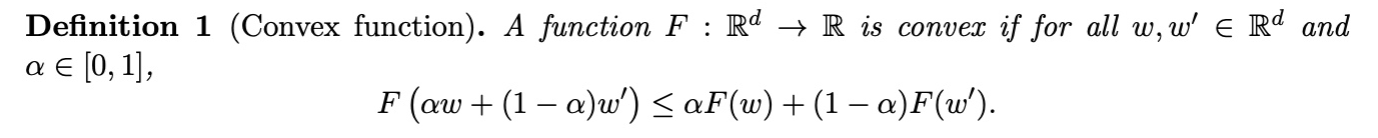
Convex Function Definition

Definition of Convex Set:

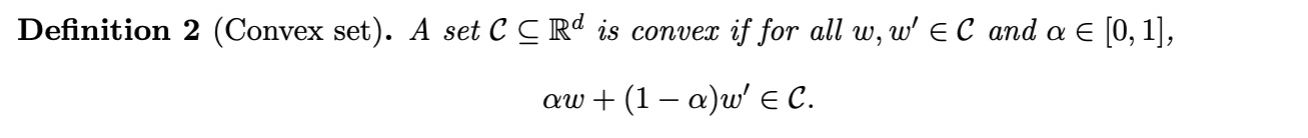
Convex Set Definition

Examples of Convex Functions:

  • l2l_2-norm: F(w)=∥x∥22=x⊤xF(w) = \|x\|_2^2=x^\top x
  • Logistic function: F(w;x,y)=log⁡(1+exp⁡(−yw⊤x))F(w;x,y)=\log(1+\exp(-yw^\top x))
  • Mean of Convex Functions: F(w)=1m∑i=1mFi(w)F(w) = \frac{1}{m}\sum_{i=1}^mF_i(w)

First and Second-Order of Convex Function

First Order

For all ω,ω′∈Rd\omega, \omega' \in \mathbb{R}^d,

F(ω′)≥F(ω)+∇F(ω)⊤(ω′−ω)F(\omega')\geq F(\omega)+\nabla F(\omega)^\top (\omega'-\omega)

Explanation: The function is above the tangent line at any point.

Second Order (Commonly used for determining convex function)

For all ω∈Rd\omega \in \mathbb{R}^d,

∇2F(ω)⪰0\nabla^2F(\omega)\succeq0

Or, the Hessian matrix ∇2F(ω)\nabla^2F(\omega) is semi-definite (PSD).

Explanation: The curvature of the function is always non-negative.

Theorem

When ww satisfies ∇F(ω)=0\nabla F(\omega)=0, ww is the global minimum of FF.

Proof:

F(w′)≥F(w)+∇F(w)⊤(w′−w)⇒F(w′)≥F(w)F(w')\geq F(w)+\nabla F(w)^\top(w'-w)\Rightarrow F(w')\geq F(w)

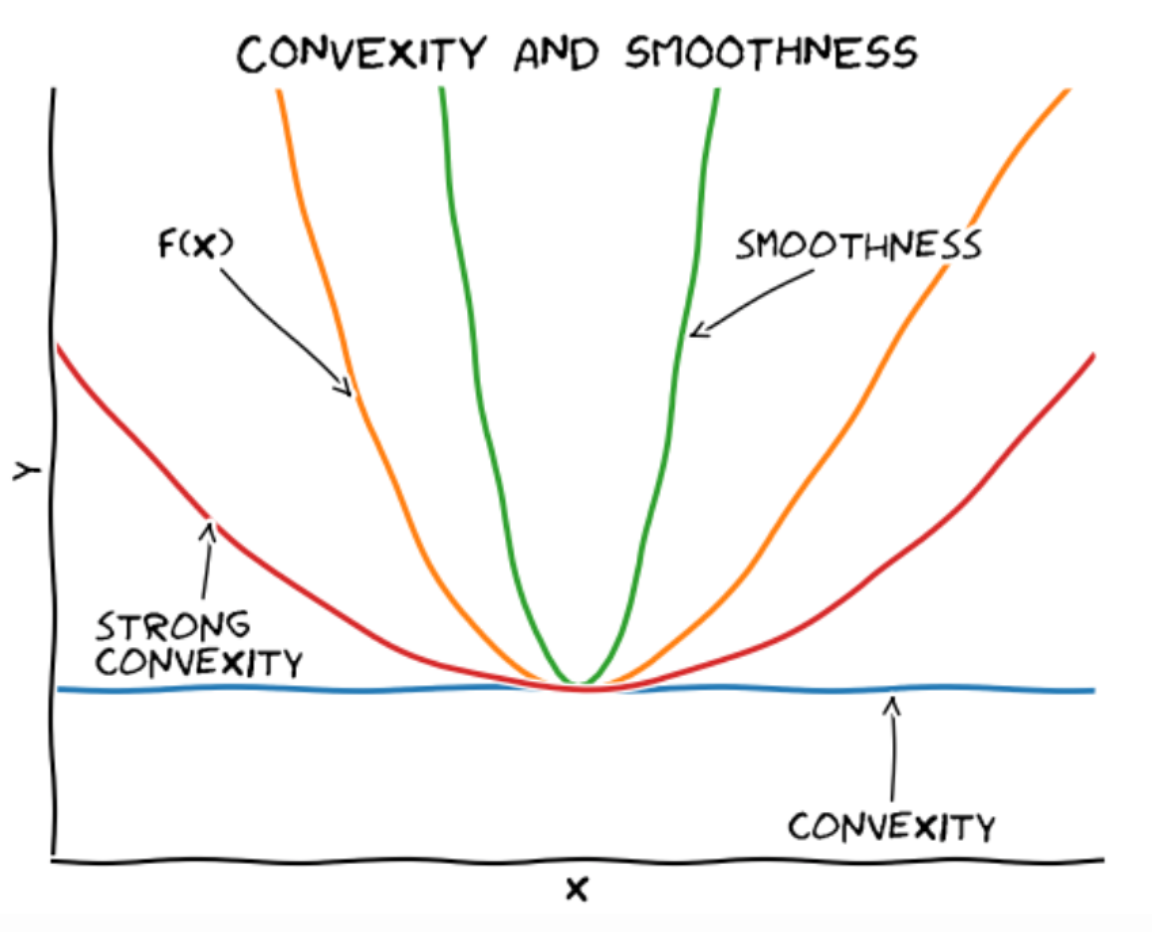
Three Bounds of Convex Functions

  • L-smooth Function (Upper Bound)

    For all w,w′∈Rdw, w' \in \mathbb{R}^d,

    F(w′)≤F(w)+∇F(w)⊤(w′−w)+L2∥w−w′∥22F(w') \leq F(w)+\nabla F(w)^\top(w'-w)+\frac{L}{2}\|w-w'\|^2_2

  • Convex Function (Lower Bound)

    For all w,w′∈Rdw, w' \in \mathbb{R}^d,

    F(w′)≥F(w)+∇F(w)⊤(w′−w)F(w') \geq F(w)+\nabla F(w)^\top(w'-w)

  • μ\mu - Strong Convex Function (Lower Bound)

    For all w,w′∈Rdw, w' \in \mathbb{R}^d,

    F(w′)≥F(w)+∇F(w)⊤(w′−w)+μ2∥w−w′∥22F(w') \geq F(w)+\nabla F(w)^\top(w'-w)+\frac{\mu}{2}\|w-w'\|^2_2

Convex Function Bounds

Gradient Descent

Algorithm Itself (GD)

Gradient Descent Algorithm

Where ηt\eta_t is called the learning rate, indicating how much to move each time. The stopping condition is generally set as F(ωt)≤ϵF(\omega_t)\leq \epsilon or ∥∇F(ωt)∥2≤ϵ\|\nabla F(\omega_t)\|_2\leq \epsilon.

Selecting Learning Rate / Step Size

Too large a learning rate can cause the results to diverge or even produce negative progress.

Too small a learning rate may take a long time to converge.

Gradient Descent for Smooth Functions

L-Smoothness Function

For all $\omega, \omega’ \in \mathbb{R}^d $,

F(w′)≤F(w)+∇F(w)⊤(w′−w)+L2∥w−w′∥22F(w')\leq F(w)+\nabla F(w)^\top (w'-w)+\frac{L}{2}\|w-w'\|^2_2

Equivalent to saying ∇F\nabla F is L-Lipschitz.

∥∇F(w)−∇F(w′)∥2≤L∥w−w′∥2\|\nabla F(w)-\nabla F(w')\|_2\leq L\|w-w'\|_2

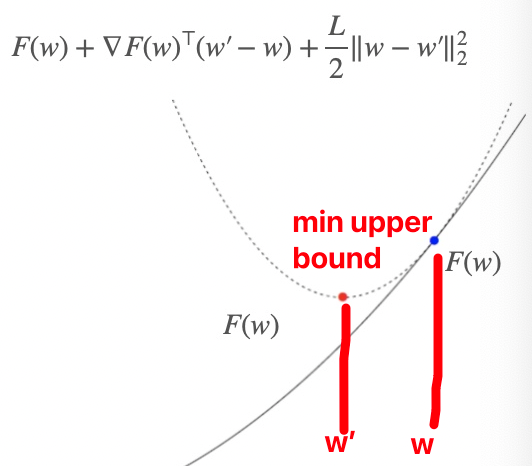
Explanation of Smoothness for Gradient Descent

To minimize FF at ww, we choose the minimum upper bound (L-smoothness), which is the following expression:

min⁡w′F(w)+∇F(w)⊤(w′−w)+L2∥w′−w∥22\min_{w'} F(w)+\nabla F(w)^\top (w'-w)+\frac{L}{2}\|w'-w\|_2^2

By setting the derivative to zero, we can obtain the next step w′w', i.e.,

w′=w−1L∇F(w)w' = w-\frac{1}{L}\nabla F(w)

By comparing the GD algorithm, we can see that this corresponds to the gradient step with a learning rate $ \eta = 1/L $.

That is, according to the upper bound, the w′w' obtained for the minimum upper bound corresponds to the lowest point of the upper bound, and its corresponding F(w′)F(w') must be smaller than F(w)F(w), thereby achieving gradient descent.

Smoothness in Gradient Descent

Convergence Proof

Theorem

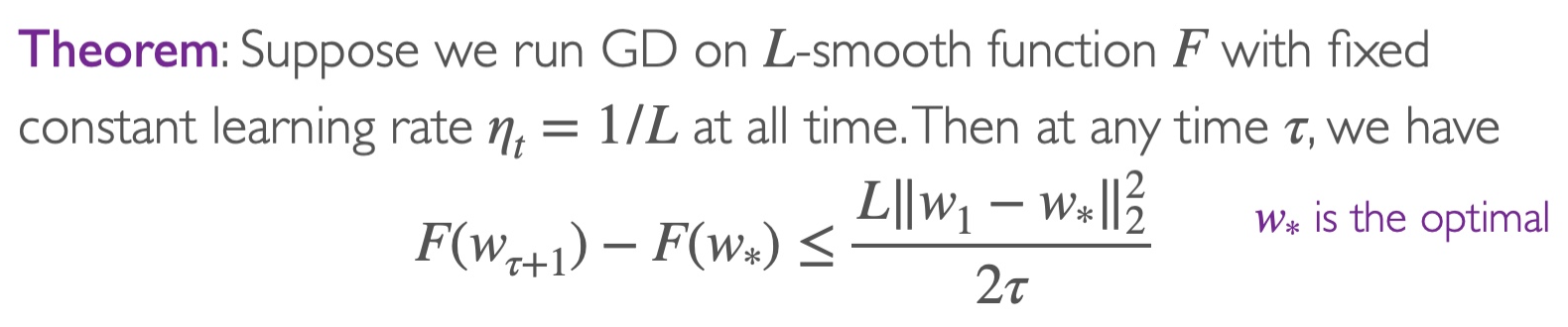
Explanation

Assuming at the beginning w1=0w_1=0 and ∥ω∗∥2=1\|\omega_*\|_2=1, then after T iterations, we have

F(wT+1)−F(ω∗)≤L2TF(w_{T+1})-F(\omega_*)\leq \frac{L}{2T}

This indicates that after T=L2ϵ=O(1/ϵ)T = \frac{L}{2\epsilon}=O(1/\epsilon) steps, we can achieve F(wT+1)−F(w∗)≤ϵF(w_{T+1})-F(w_*)\leq \epsilon. Hence, we say that gradient descent has a convergence rate of O(1/T)O(1/T).

Proof

For the specific proof, refer to the attached PDF (Lec10-2).

Gradient Descent on Smooth and Strongly Convex Functions

μ\mu- Strongly Convex Function

For all ω,ω′∈Rd\omega, \omega' \in \mathbb{R}^d,

Lower bound of F(w)

F(w′)≥F(w)+∇F(w)⊤(w′−w)+μ2∥w−w′∥22F(w')\geq F(w)+\nabla F(w)^\top (w'-w)+\frac{\mu}{2}\|w-w'\|^2_2

Convergence Proof

Theorem

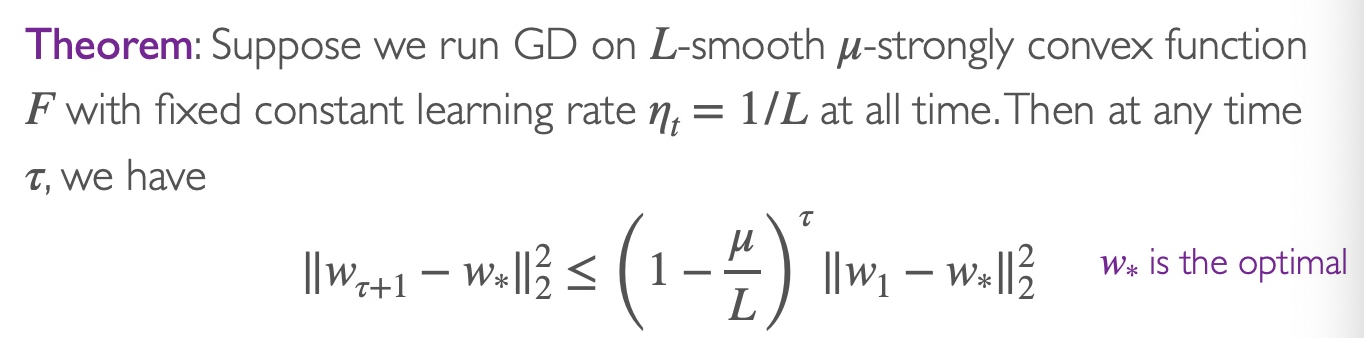
Explanation

Assuming at the beginning w1=0w_1=0 and ∥ω∗∥2=1\|\omega_*\|_2=1, then after T iterations, we have

∥wT+1−w∗∥22≤(1−μL)⊤\|w_{T+1}-w_*\|_2^2\leq (1-\frac{\mu}{L})^\top

This indicates that after T=Lμlog⁡(1/ϵ)=O(log⁡(1/ϵ))T = \frac{L}{\mu}\log(1/\epsilon)=O(\log(1/\epsilon)) steps, we can achieve ∥wT+1−w∗∥2≤ϵ\|w_{T+1}-w_*\|_2\leq \epsilon. Hence, we say that gradient descent has a convergence rate of O(exp⁡(−T))O(\exp(-T)).

Appendix

GD converge with L smooth and F proof

Step 1

Based on the smoothness Equation 1, at time t,

F(wt+1)−F(wt)≤∇F(wt)⊤(wt+1−wt)+L2∥wt+1−wt∥22F(w_{t+1})-F(w_t)\leq \nabla F(w_t)^\top(w_{t+1}-w_t)+\frac{L}{2}\|w_{t+1}-w_t\|^2_2

Substituting ∇F(wt)=L(wt−wt+1)\nabla F(w_t) = L(w_t-w_{t+1}) into Equation (4),

F(wt+1)−F(wt)≤L(wt−wt+1)⊤(wt+1−wt)+L2∥wt+1−wt∥22=−L(wt+1−wt)⊤(wt+1−wt)+L2∥wt+1−wt∥22=−L∥wt+1−wt∥22+L2∥wt+1−wt∥22=−L2∥wt+1−wt∥22\begin{aligned} F(w_{t+1})-F(w_t) &\leq L(w_{t}-w_{t+1})^\top(w_{t+1}-w_t)+\frac{L}{2}\|w_{t+1}-w_t\|^2_2\\ &= -L(w_{t+1}-w_{t})^\top(w_{t+1}-w_t)+\frac{L}{2}\|w_{t+1}-w_t\|^2_2\\ & =-L \|w_{t+1}-w_t\|_2^2+\frac{L}{2}\|w_{t+1}-w_t\|^2_2\\ & =-\frac{L}{2}\|w_{t+1}-w_t\|^2_2 \end{aligned}

Step 2

Based on convex function Equation 2 and ∇F(wt)=L(wt−wt+1)\nabla F(w_t) = L(w_t-w_{t+1}), we obtain

F(w∗)≥F(w)+∇F(w)⊤(w∗−w)⇒F(wt)−F(w∗)≤L(wt−wt−1)⊤(wt−w∗) \begin{aligned} F(w_*) &\geq F(w)+\nabla F(w)^\top(w_*-w)\\ \Rightarrow F(w_t)-F(w_*)&\leq L(w_t-w_{t-1})^\top(w_t-w_*) \end{aligned}

And as

∥wt+1−w∗∥22=∥wt+1−wt+wt−w∗∥22=∥wt+1−wt∥22+∥wt−w∗∥22+2(wt+1−wt)⊤(wt−w∗) \begin{aligned} \|w_{t+1}-w_*\|_2^2&=\|w_{t+1}-w_t+w_t-w_*\|_2^2\\ & = \|w_{t+1}-w_t\|_2^2+\|w_{t}-w_*\|_2^2+2(w_{t+1}-w_t)^\top(w_t-w_*) \end{aligned}

Substituting Equation (7) into Equation (6), we get

F(wt)−F(w∗)≤L2(∥wt+1−wt∥22+∥wt−w∗∥22−∥wt+1−w∗∥22) \begin{aligned} F(w_t)-F(w_*)&\leq \frac{L}{2}(\|w_{t+1}-w_t\|_2^2+\|w_t-w_*\|_2^2-\|w_{t+1}-w_*\|_2^2) \end{aligned}

Substituting Equation (5) into Equation (8)

F(wt+1)−F(wt)+F(wt)−F(w∗)≤L2(∥wt−w∗∥22−∥wt+1−w∗∥22)≤L2∥wt−w∗∥22 \begin{aligned} F(w_{t+1})-F(w_t)+F(w_t)-F(w_*)&\leq \frac{L}{2}(\|w_t-w_*\|_2^2 - \|w_{t+1}-w_*\|_2^2) \\ &\leq\frac{L}{2}\|w_t-w_*\|_2^2 \end{aligned}

Step 3

Based on Equation 9, summing from tau+1 to tau yields

F(wτ+1)−F(w∗)+F(wτ+1)−F(w∗)+...+F(wτ+1)−F(w∗)=τ(F(wτ+1)−F(w∗))≤F(wτ+1)−F(w∗)+F(wτ)−F(w∗)+...+F(w1)−F(w∗)=∑t=1τ(F(wt+1)−F(w∗))≤L2(∥wτ−w∗∥22−∥wτ+1−w∗∥22+∥wτ−1−w∗∥22−∥wτ−w∗∥22)+...+∥w1−w∗∥22−∥w2−w∗∥22)≤L2(∥w1−w∗∥22−∥wτ+1−w∗∥22)≤L2∥w1−w∗∥22\begin{aligned} &F(w_{\tau+1})-F(w_*)+F(w_{\tau+1})-F(w_*)+...+F(w_{\tau+1})-F(w_*) = \tau(F(w_{\tau+1})-F(w_*))\\ &\leq F(w_{\tau+1})-F(w_*)+F(w_\tau)-F(w_*)+...+F(w_1)-F(w_*)=\sum_{t=1}^\tau(F(w_{t+1})-F(w_*))\\ &\leq \frac{L}{2}(\|w_\tau-w_*\|^2_2-\|w_{\tau+1}-w_*\|_2^2+\|w_{\tau-1}-w_*\|^2_2-\|w_{\tau}-w_*\|_2^2)+...+\|w_1-w_*\|_2^2-\|w_2-w_*\|_2^2)\\ &\leq \frac{L}{2}(\|w_1-w_*\|_2^2-\|w_{\tau+1}-w_*\|_2^2) \\ &\leq\frac{L}{2}\|w_1-w_*\|_2^2 \end{aligned}

Substituting w1=0w_1=0 and ∥w∗∥22=1\|w_*\|_2^2=1, after T iterations (i.e., τ=T\tau=T), we get

F(wT+1)−F(w∗)≤L2TF(w_{T+1})-F(w_*)\leq \frac{L}{2T}

This indicates that after T=L2ϵT=\frac{L}{2\epsilon} iterations, function F converges, i.e., F(wT+1)−F(w∗)≤ϵF(w_{T+1})-F(w_*)\leq \epsilon

Comparison of Different Gradient Descent Algorithms (Not part of the course requirements)

Batch Gradient Descent | Standard Gradient Descent | Batch GD

Computes gradient using all samples every time (i=1～n)

f(x)=1n∑i=1nfi(x)∇f(x)=1n∑i=1n∇fi(x)f(x) = \frac{1}{n}\sum_{i=1}^nf_i(x)\\ \nabla f(x)=\frac{1}{n}\sum_{i=1}^n \nabla f_i(x)

Advantages: Accurate gradient update

Disadvantages: Only guarantees global optimum for convex function; slow convergence

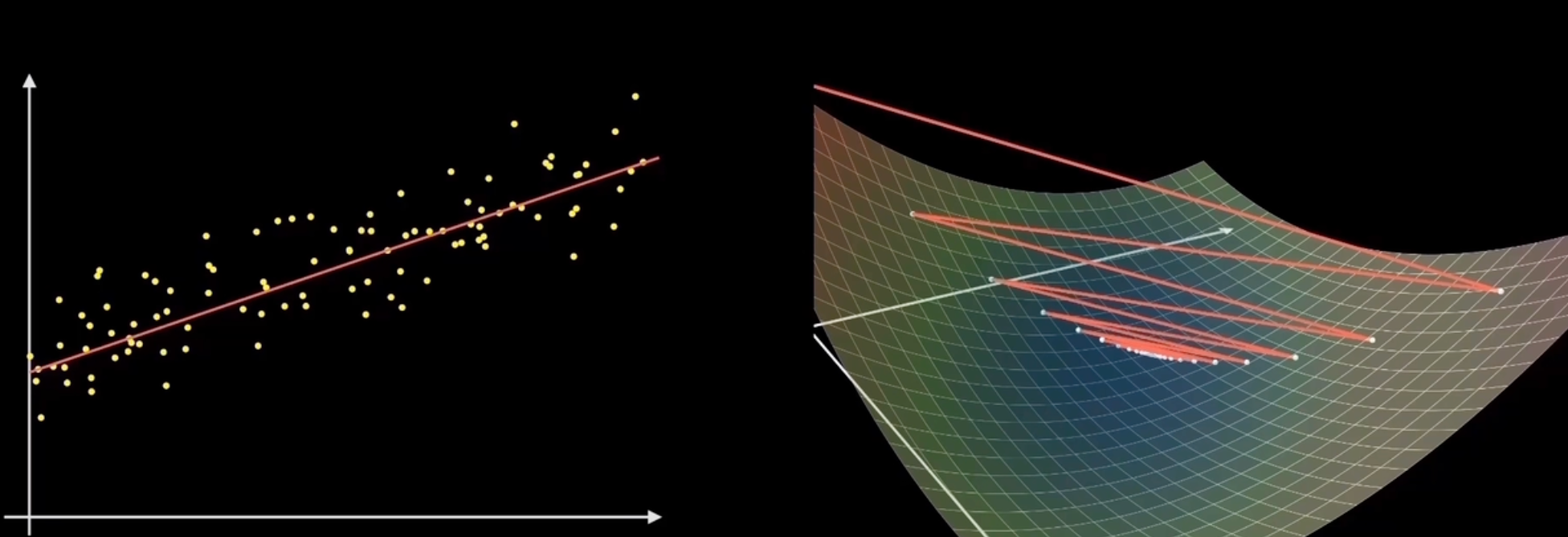
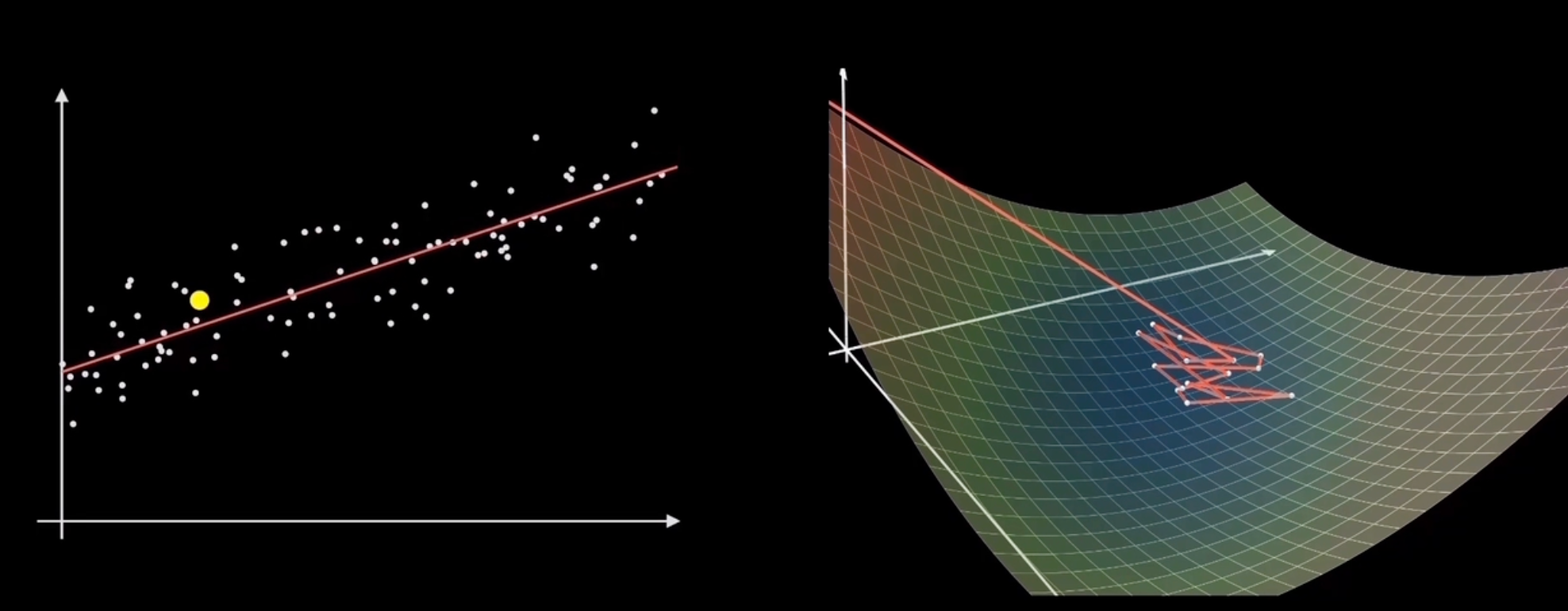
Stochastic Gradient Descent | Stochastic GD

Computes gradient using only one sample point every time (i is any value from 1 to n, randomly chosen)

f(x)=fi(x)∇f(x)=∇fi(x)f(x) = f_i(x)\\ \nabla f(x)=\nabla f_i(x)

Advantages: Fast training speed

Disadvantages: Tends to jump around near the optimum, might not reach the optimum; limited to the vicinity of the optimal point

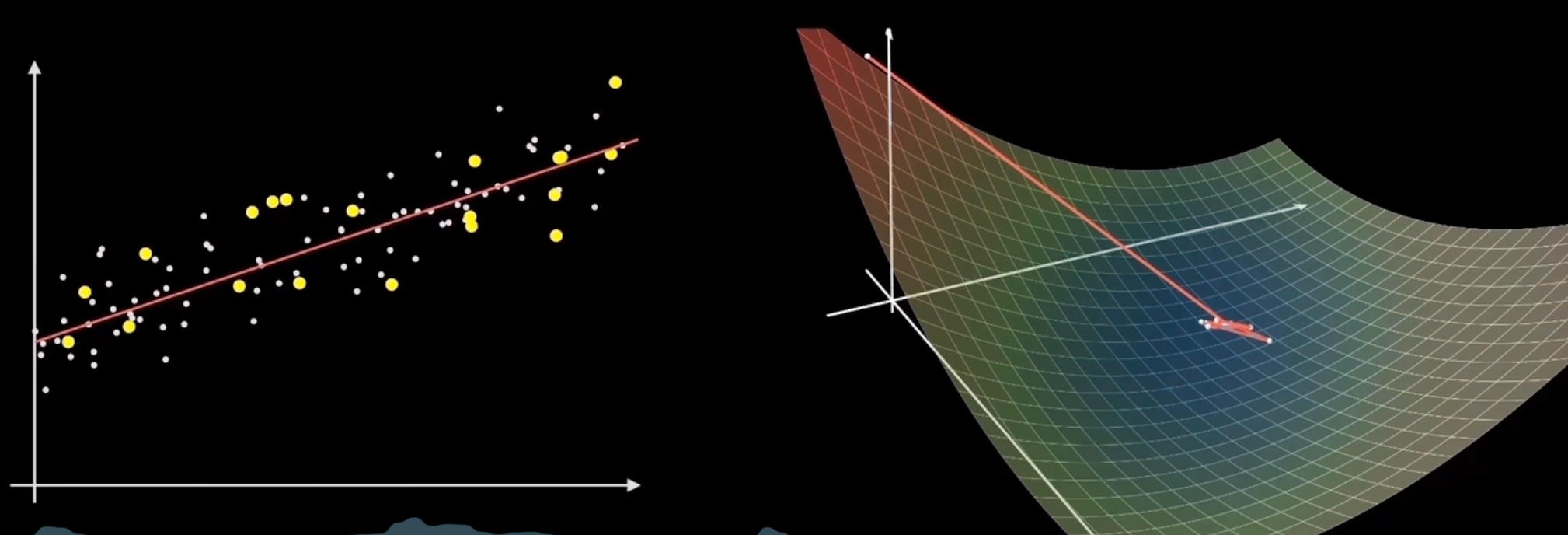
Mini-Batch Gradient Descent | Mini-Batch GD

Computes gradient using a batch of sample points every time (selects k samples randomly from n samples)

f(x)=1k∑i=1kfi(x)∇f(x)=1k∑i=1k∇fi(x)f(x) = \frac{1}{k}\sum_{i=1}^kf_i(x)\\ \nabla f(x)=\frac{1}{k}\sum_{i=1}^k \nabla f_i(x)

Advantages: Faster training speed

Disadvantages: Chooses the direction of the smallest average gradient

Note: The content in this blog is class notes shared for educational purposes only. Some images and content are sourced from textbooks, teacher materials, and the internet. If there is any infringement, please contact aursus.blog@gmail.com for removal.