Fourier Transform

Mathematical Definitions

Discrete Fourier Transform (DFT) Definition:

Fn=∑k=0N−1fke−2πink/NF_n= \sum_{k=0}^{N-1} f_k e^{-2\pi ink/N}

Continuous Fourier Transform (CFT) Definition:

F(v)=∫−∞+∞f(t)e−2πivtdtF(v)=\int_{-\infty}^{+\infty} f(t)e^{-2\pi ivt}dt

Discrete Inverse Fourier Transform (IDFT) Definition:

fk=1n∑n=0N−1Fne2πink/Nf_k= \frac{1}{n}\sum_{n=0}^{N-1} F_n e^{2\pi ink/N}

Continuous Inverse Fourier Transform (CIFT) Definition:

f(t)=∫−∞+∞F(v)e2πivtdvf(t)=\int_{-\infty}^{+\infty} F(v)e^{2\pi ivt}dv

Explanation and Understanding

The purpose of the Fourier Transform is to decompose a signal into its frequency components.

This is achieved by constructing a series of sinusoidal waves with different frequencies and performing dot products with the original signal.

Signals are transformed from the time-domain to the frequency-domain through the Fourier Transform and can be transformed back to the time-domain through the Inverse Fourier Transform.

Q: Why do we use the complex form of signals?

When sinusoidal waves with similar frequencies and phase are multiplied, the result’s amplitude is maximal. However, if the waves have the same frequency but a phase difference of π/2\pi/2, the direct product results in 0.

To avoid this, signals are transformed into complex numbers, comprising real and imaginary parts. Multiplying a complex signal by a sinusoidal wave of a certain frequency ensures that the result is not affected by the phase difference.

Using Euler’s Formula, we represent complex sinusoidal waves as vectors:

Ae2πft=A[cos⁡(2πft)+isin⁡(2πft)]Ae^{2\pi ft}=A[\cos (2\pi ft) +i\sin(2\pi ft)]

Where A represents amplitude (length of the vector) and f represents the rotating frequency.

Sinusoidal Wave Frequencies Selection:

As per the Nyquist theorem, the maximum frequency we can measure is half of the sampling frequency.

Hence, for a Discrete Fourier Transform result’s length of N, we need N different frequencies of sinusoidal waves to completely extract the signal.

If the signal has only a real part, we need N/2+1N/2+1 different frequencies of sinusoidal waves to extract the signal.

Code

fft｜Fast Fourier Transform

The fft significantly reduces the time required for Fourier Transform.

MATLAB Code

1
2
3
4
5
6
7
% FFT Usage
dataFFT = fft(data); % Performs FFT on 'data'
% 'dataFFT' has a length of 1xN, containing N/2+1 unique frequencies (from 0 to fs/2)

% Plotting the frequency domain
fVec = linspace(0, fs/2, N/2+1); % Creates a frequency vector
plot(fVec, abs(dataFFT(1:(N/2+1)))); % Plots non-zero frequencies (positive frequency)
1
2
3
4
5
% Adding NFFT (FFT Length)
dataFFT = fft(data, NFFT); % 'NFFT' represents the FFT length
% If NFFT > N, zero-padding is applied to the end of 'data'; if NFFT < N, some points are removed from the end of 'data'
fVec = linspace(0, fs/2, NFFT/2+1); % Creates a frequency vector
plot(fVec, abs(dataFFT(1:(NFFT/2+1)))); % Plots non-zero frequencies (positive frequency)
1
2
3
% IFFT Usage
dataFFT = fft(data);
data = ifft(dataFFT); % Performs IFFT on 'dataFFT' to recover the original signal 'data'

Python Code

1
2
3
4
dataFFT = np.fft.fft(data) # Perform FFT on data
fVec = np.linspace(0, fs/2, N//2+1)  # Construct frequency vector
plt.plot(fVec, np.abs(dataFFT[0:N//2+1]))  # Plot positive frequencies
plt.show()

Exercise

Problem Statement:

Manually create a Discrete Fourier Transform (DFT). Signal X has a length of N and a sampling frequency (fs) of fs.

Hints:

  1. Extract (N/2)+1 independent frequencies, with the maximum value being fs/2.
  2. Euler’s Formula: Ae2πft=A[cos⁡(2πft)+isin⁡(2πft)]Ae^{2\pi ft}=A[\cos (2\pi ft) +i\sin(2\pi ft)]

Available functions: exp(t), a+bi, linspace()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
N = 1000; % Length of signal
fs = 200; % Sampling frequency
time = (1:N)/fs; % Time vector
X = sin(2*pi*10*time) + 0.5*cos(2*pi*37*time); % Our signal

% Frequency information
nFrequency = N/2 + 1; % # of frequencies we can extract (including 0)
nyquist = fs/2; % Nyquist frequency
frequencies = linspace(0,nyquist,nFrequency); % Frequency vector

% Initialize Fourier coefficients
fourier = zeros(1,nFrequency);

% Fourier transform
for i=1:nFrequency
  sine_wave = exp(-1i*2*pi*frequencies(i).*time); % Constructing the sine wave
  fourier(i) = sine_wave*X'; % Fourier transform is the dot product of the original signal X and the sine wave family
end

% Plot the magnitude of the Fourier coefficients
figure; plot(frequencies, abs(fourier))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

N = 1000  # Length of signal
fs = 200  # Sampling frequency
time = np.arange(1, N+1) / fs  # Time vector
X = np.sin(2*np.pi*10*time) + 0.5*np.cos(2*np.pi*37*time)  # Our signal

# Frequency information
nFrequency = N//2 + 1  # # of frequencies we can extract (including 0)
nyquist = fs/2  # Nyquist frequency
frequencies = np.linspace(0, nyquist, nFrequency)  # Frequency vector

# Initialize Fourier coefficients
fourier = np.zeros(nFrequency, dtype=np.complex128)

# Fourier transform
for i in range(nFrequency):
    sine_wave = np.exp(-1j*2*np.pi*frequencies[i]*time)  # Construct sine wave
    fourier[i] = np.dot(sine_wave, X)  # Fourier transform as dot product of X and sine wave

# Plot the magnitude of the Fourier coefficients
plt.figure()
plt.plot(frequencies, np.abs(fourier))
plt.show()

Short-time Fourier Transform | STFT

Due to the limitations of the Fourier Transform in handling unstable signals (unstationary signals), we employ the Short-time Fourier Transform. Reducing the window length can improve spatial resolution, but if it’s too small, it may result in poor frequency resolution.

Q: What can be done if there are edge artifacts or spectral leakage?

If the signal exhibits edge artifacts or spectral leakage, we use tapering to modulate the signal. Common tapering methods include using the Hann window, Hamming window, or Gaussian window. Generally, the Hann window can alleviate edge effects.

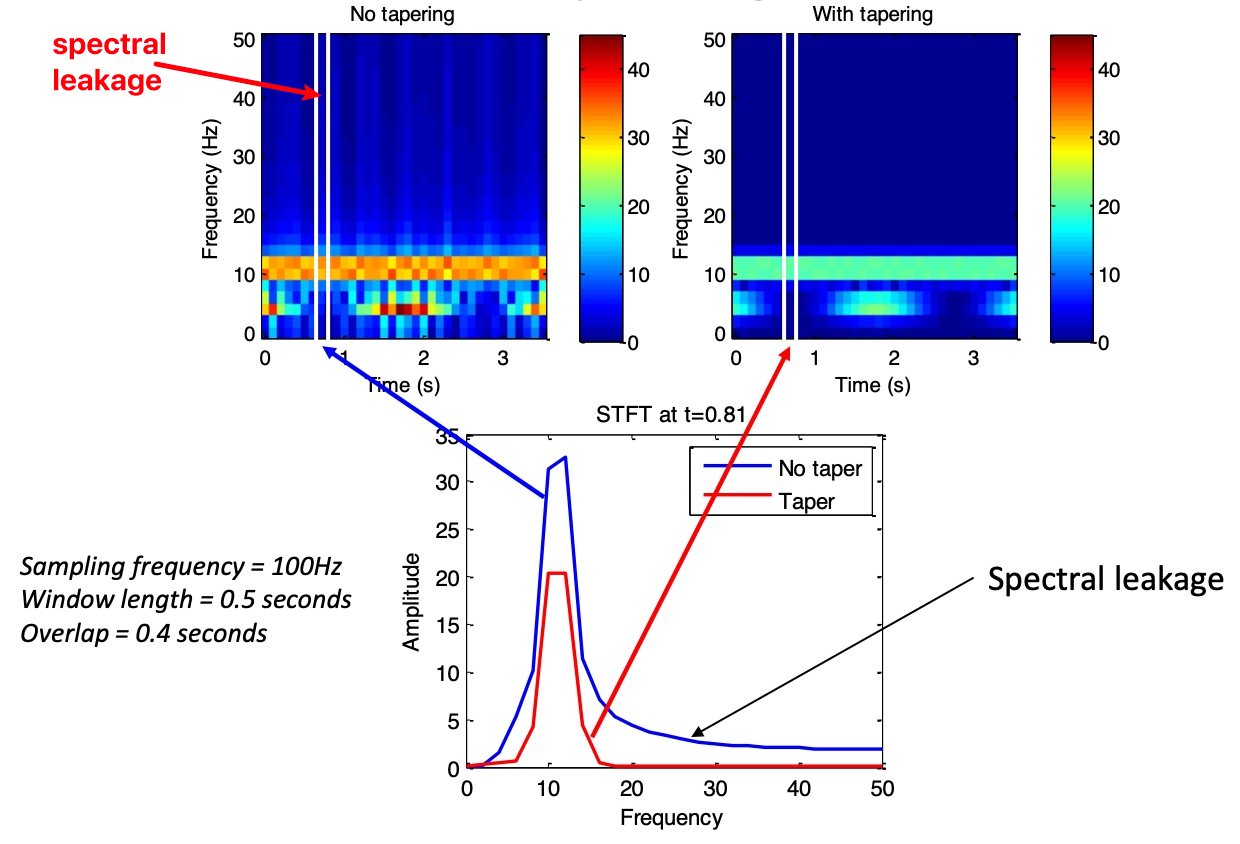
Edge Artifacts

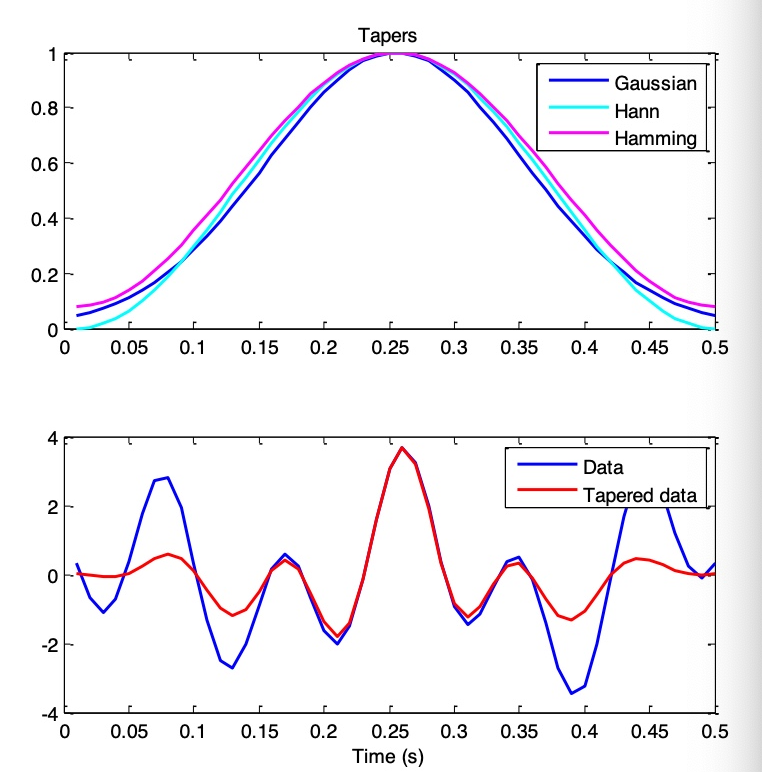
Spectral Leakage

Q: How should the parameters be set?

Time segment length: It’s usually preferable to have segments that can encompass 2-3 cycles. Longer segments → higher frequency resolution; shorter segments → higher time resolution.

Overlap: Typically set to 50%-90%.

Appendix:

Understanding Fourier Transform: https://zhuanlan.zhihu.com/p/19759362

Note: The content in this blog is class notes shared for educational purposes only. Some images and content are sourced from textbooks, teacher materials, and the internet. If there is any infringement, please contact aursus.blog@gmail.com for removal.