生物医学工程 | EEG分析 - 卷积和点成
点乘|Dot Product
数学定义
假设输入为两个vector,,,则点乘结果为
代码
MATLAB代码
1 | z = dot(x,y) |
Python代码
1 | z = np.dot(x, y) |
卷积|Convolution
数学定义
离散卷积定义
假设输入为两个vector,,,则点乘结果为
连续卷积定义
假设输入为两个连续函数和,则点乘结果为
解释和理解
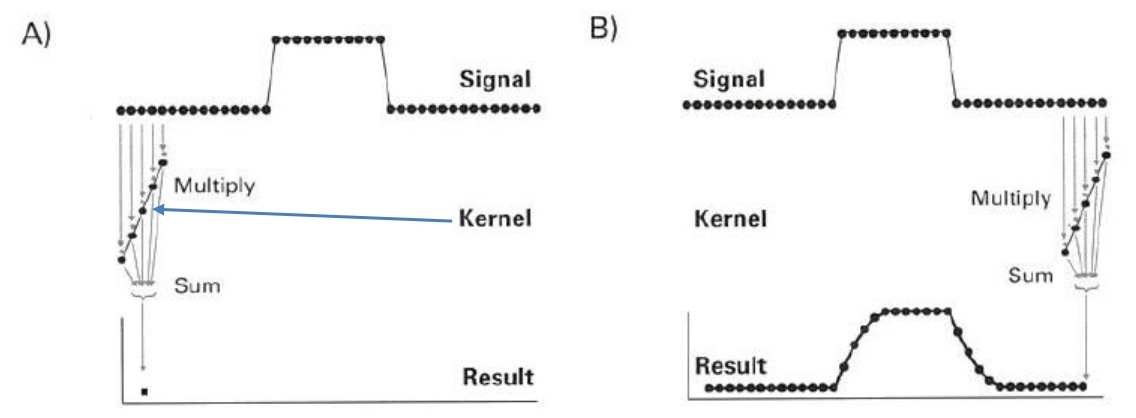
通常我们将x称为信号,h称为卷积核kernel,通常卷积核的长度比信号短一些。
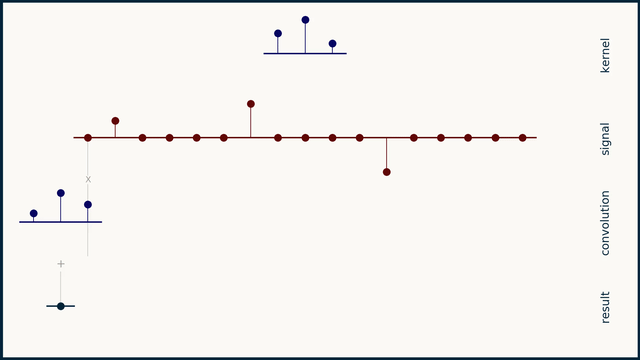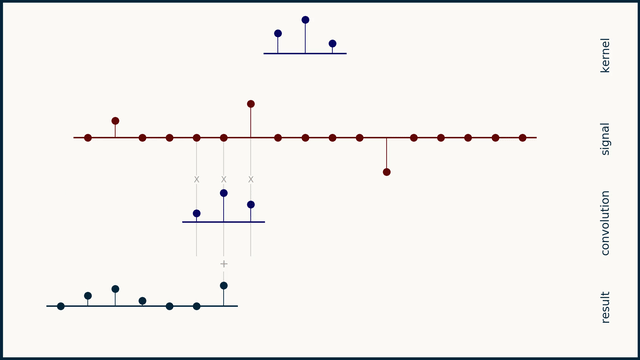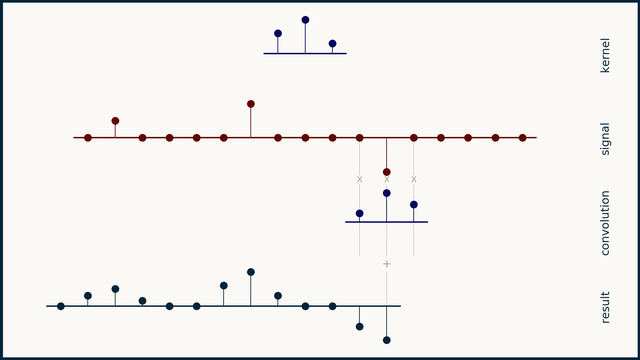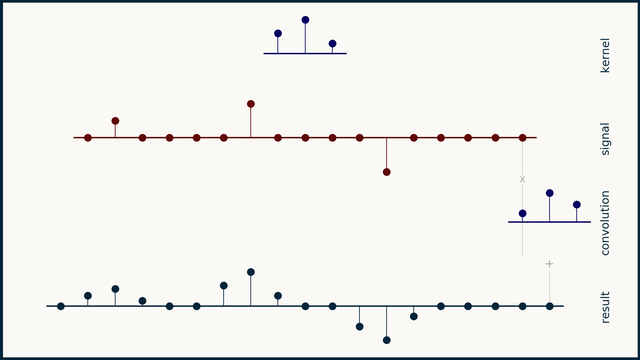
离散卷积:如果信号x和卷积核h都是离散的,则卷积可以理解为卷积核h从信号的一侧取长度和卷积核h一样的一组数据点,然后一一对应的进行点乘,并将结果求和作为第一个卷积的结果。然后卷积核h在信号上向右滑动一格,重复上面的步骤得到第二个卷积结果,以此类推直到卷积核遍历了信号x的所有点。
连续卷积:如果信号x和卷积核h都是连续的,则卷积可以理解为卷积核h和信号x重合的面积,并将面积的大小作为第一个卷积的结果。然后卷积核h在信号上向右滑动,重复上面的步骤得到第二个卷积结果,以此类推直到卷积核遍历了信号x的所有点。
从理论上来讲,卷积核是从负无穷滑动到正无穷。但通常我们只取信号x不为零的部分。需要注意的是,卷积之后可能需要人工选择长度,不论是matlab还是python都给出了卷积结果长度选项,但我们也可以手动截取某一个部分
 |
 |
 |
 |
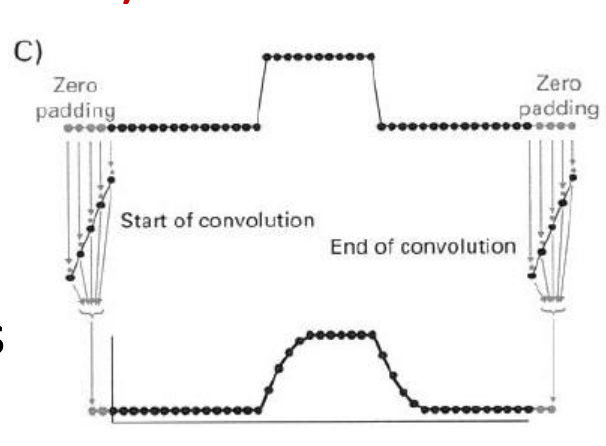
为了保证信号两端的点都能够被卷积核完整的覆盖到,我们通常会给信号两端加一些为零的点(见图C)。补零之后卷积结果的长度为**信号长度+卷积核长度-1**。卷积之后的幅度会改变,如果想要和原始信号的幅值进行比较的话,则只需要将卷积结果除以卷积核的长度即可。此外,一般推荐卷积核选择奇数作为长度。
点积和卷积的区别
-
点积(dot product)在数学上与相关系数(correlation coefficient)相关联,它用于衡量两个信号之间的相似性,而不考虑时间偏移。
傅里叶变换(Fourier Transform)可以提供信号的频谱信息,并在频域中比较信号的相似性。
-
卷积(convolution)在数学上与交叉相关(cross-correlation)相关联,用于衡量信号在时间上的相似性随时间偏移的变化。
小波变换(Wavelet Transform)可以提供不同尺度和时间分辨率下信号的特征信息,并比较信号在不同时间上的相似性。
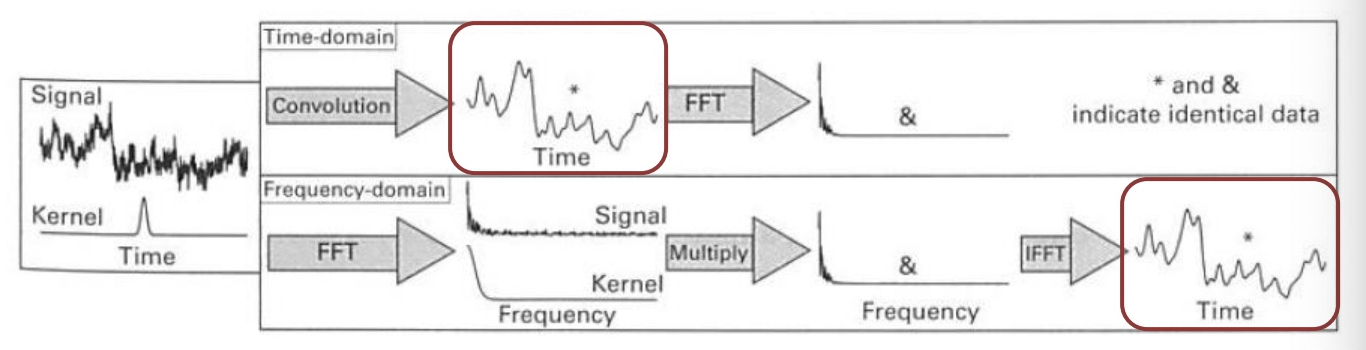
时域的卷积等价于频域的点积。换句话说,以下两种方法得出的结果相同
代码
MATLAB代码
1 | y = conv(u,h) % 等价于conv(h,u) |
Python代码
1 | y = np.convolve(u, h) # 等价于conv(h,u) |
!练习
题目:使用一个长度为11的卷积核对信号求移动平均(类似移动平均滤波器)
1 | x = cumsum(randn(1,1000)) |
1 | import numpy as np |
声明:此blog内容为上课笔记,仅为分享使用。部分图片和内容取材于课本、老师课件、网络。如果有侵权,请联系aursus.blog@gmail.com删除。